如图，四边形ABCD中，E、F、G、日分别为各边的中点，顺次连结E、F、G、H，把四边形EFGH称为中点四边形．连结AC、BD，容易证明：中点四边形EFGH一定是平行四边形．

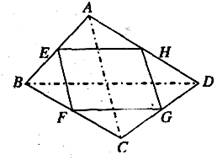
    (1)如果改变原四边形ABCD的形状，那么中点四边形的形状也随之改变，通过探索可以发现：当四边形ABCD的对角线满足AC=BD时，四边形EFGH为菱形；

    当四边形ABCD的对角线满足_____________时，四边形EFGH为矩形；

    当四边形ABCD的对角线满足_____________时，四边形EFGH为正方形．

    (2)探索△AEH、△CFG与四边形ABCD的面积之间的等量关系，请写出你发现的结论，并加以证明．

    (3)如果四边形ABCD的面积为2．那么中点四边形EFGH的面积是多少?

如图，O₁与O₂相交于点A、B，顺次连结O₁、A、O₂、B4点，得四边形O₁AO₂B．

(1)根据我们学习矩形、菱形、正方形性质时所获得的经验，探求图中的四边形有哪些性质？(用文字语言写出4条性质)

性质1：________________________________；

性质2：________________________________；

性质3：________________________________；

性质4：________________________________．

(2)设O₁的半径为R，O₂的半径为r(R＞r)，O₁、O₂的距离为d．当d变化时，四边形O₁AO₂B的形状也会发生变化．要使四边形O₁AO₂B是凸四边形(把四边形的任一边向两方延长，其他各边都在延长所得直线同一旁的四边形)，则d的取值范围是________________．

如图：四边形ABCD中，E、F、G、H分别为各边的中点，顺次连接E、F、G、H，把四边形EFGH称为中点四边形．连接AC、BD，容易证明：中点四边形EFGH一定是平行四边形．
（1）如果改变原四边形ABCD的形状，那么中点四边形的形状也随之改变，通过探索可以发现：当四边形ABCD的对角线满足AC=BD时，四边形EFGH为菱形．
当四边形ABCD的对角线满足时，四边形EFGH为矩形；
当四边形ABCD的对角线满足时，四边形EFGH为正方形；
（2）探索三角形AEH、三角形CFG与四边形ABCD的面积之间的等量关系，请写出你发现的结论，并加以证明；
（3）如果四边形ABCD的面积为2，那么中点四边形EFGH的面积是多少？