
题目列表(包括答案和解析)
(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=![]() ,其中
,其中![]() 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3) 拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.
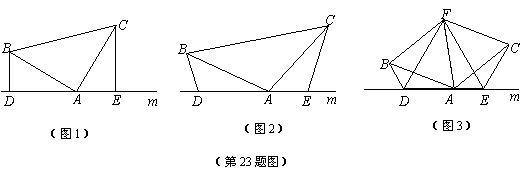 |
 ,BC为⊙O的直径, AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F.
,BC为⊙O的直径, AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F.
 ,求⊙O的直径BC.
,求⊙O的直径BC.(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=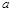 ,其中
,其中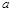 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.
(10分) 如图9,已知,在△ABC中,∠ABC=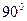 ,BC为⊙O的直径, AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F.
,BC为⊙O的直径, AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F.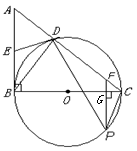
(1)求证:ED是⊙O的切线.
(2)如果CF ="1,CP" =2,sinA =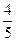 ,求⊙O的直径BC.
,求⊙O的直径BC.

![]() 如图,已知:在△ABC中,∠BAC=90°,延长BA到点D,使
如图,已知:在△ABC中,∠BAC=90°,延长BA到点D,使![]() ,点G、E、F分别为边AB、BC、AC的中点.求证:DF=BE。
,点G、E、F分别为边AB、BC、AC的中点.求证:DF=BE。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com