
题目列表(包括答案和解析)
已知:在四边形ABCD中,AB=CD,BC=AD,E、F是对角线AC上两点,且AE=CF.
求证:BE=DF.

已知,在四边形ABCD中,AB=DC、AD=BC,点E在BC上,点F在AD上,AF=CE,EF与对角线BD相交于O.
求证:O是BD中线.
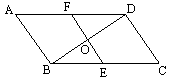
已知:在四边形ABCD中,AD∥BC,∠BAC=∠D,点E、F分别在BC、CD上,且∠AEF=∠ACD,试探究AE与EF之间的数量关系。
(1)如图1,若AB=BC=AC,则AE与EF之间的数量关系是什么;
(2)如图2,若AB=BC,你在(1)中得到的结论是否发生变化?写出猜想,并加以证明;
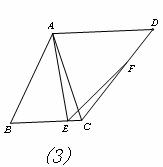
(3)如图3,若AB=kBC,你在(1)中得到的结论是否发生变化?写出猜想不用证明。

已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.

1.(1)设AE=x,四边形AMND的面积为 S,求 S关于x 的函数解析式,并指明该函数的定义域;
2.(2)当AM为何值时,四边形AMND的面积最大?最大值是多少?
3.(3)点M能是AB边上任意一点吗?请求出AM的取值范围.

 为 S,求 S关于x 的函数解析式,并指明该函数的定义域;
为 S,求 S关于x 的函数解析式,并指明该函数的定义域;湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com