
题目列表(包括答案和解析)
如图,![]() 的直径,
的直径,![]() 、
、![]() 是圆周上关于
是圆周上关于![]() 对称的两个不同点,
对称的两个不同点,![]() .
.
(1)![]() 在
在![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]()
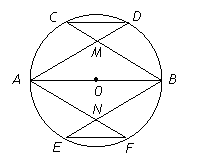
![]() 六点中,能构成矩形的四个点有哪些?请一一列出(不要求证明);
六点中,能构成矩形的四个点有哪些?请一一列出(不要求证明);
(2)求证:四边形![]() 是菱形.
是菱形.
 |
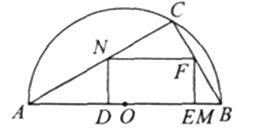
在直径为AB的半圆内,划出一块三角形区域,使三角形的一边为AB,顶点C在半圆上,AC=8,BC=6.现要建造一个内接于△ABC的矩形水池DEFN,其中D、E在AB上,如图3-C-27所示的设计方案.
(1)求△ABC中AB边上的高h;
(2)已知△CFN的边FN上的高与h的比等于![]() ,设DN=x,当x为何值时,水池DEFN的面积最大?
,设DN=x,当x为何值时,水池DEFN的面积最大?
(3)实际施工时,发现AB边上距离B点1.85的M处有一棵大树,问:这棵大树是否位于矩形水池的边上?如果在,为了保护大树,请设计出另外的方案,使内接于三角形中欲建的满足条件的最大矩形水池能避开大树.
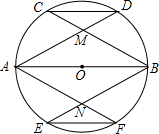 M,AF与BE交于N.
M,AF与BE交于N.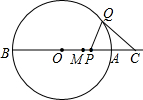 如图,AB是⊙O的直径,点M是半径OA的中点,点P在线段AM上运动(不与点M重合).点Q在上半圆上运动,且总保持PQ=PO,过点Q作⊙O的切线交BA的延长线于点C.
如图,AB是⊙O的直径,点M是半径OA的中点,点P在线段AM上运动(不与点M重合).点Q在上半圆上运动,且总保持PQ=PO,过点Q作⊙O的切线交BA的延长线于点C.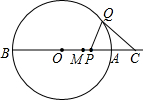 且总保持PQ=PO,过点Q作⊙O的切线交BA的延长线于点C.
且总保持PQ=PO,过点Q作⊙O的切线交BA的延长线于点C.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com