
题目列表(包括答案和解析)
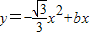 经过点B,求此抛物线函数解析式;
经过点B,求此抛物线函数解析式;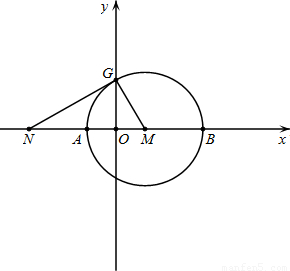
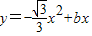 经过点B,求此抛物线函数解析式;
经过点B,求此抛物线函数解析式;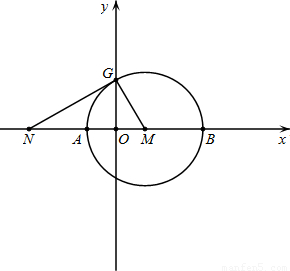
如图,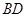 为⊙
为⊙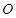 的直径,
的直径,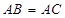 ,
,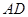 交
交 于点
于点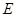 ,
,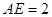 ,
,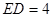 .
.
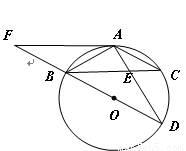
(1)求证: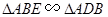 ;
;
(2)求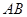 的长;
的长;
(3)延长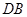 到
到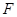 ,使得
,使得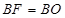 ,连接
,连接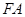 ,试判断直
线
,试判断直
线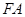 与⊙
与⊙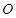 的位置关系,并说明理由.
的位置关系,并说明理由.
【解析】(1)根据AB=AC,可得∠ABC=∠C,利用等量代换可得∠ABC=∠D然后即可证明△ABE∽△ADB.
(2)根据△ABE∽△ADB,利用其对应边成比例,将已知数值代入即可求得AB的长.
(3)连接OA,根据BD为⊙O的直径可得∠BAD=90°,利用勾股定理求得BD,然后再求证∠OAF=90°即可
| 3 |
| 2 |
| 3 |
| 2 |
| 4 |
| 3 |
| 4 |
| 3 |
| a |
| a-1 |
| a |
| b |
| b |
| a |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com