
题目列表(包括答案和解析)
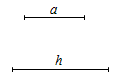
 ,其底边长为x cm,底边上的高为y cm,求y关于x的函数关系式,并作出此函数的图像。
,其底边长为x cm,底边上的高为y cm,求y关于x的函数关系式,并作出此函数的图像。
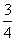 x+3 , l2:y=-3x+3,若l2上的一点M到l1的距离是
x+3 , l2:y=-3x+3,若l2上的一点M到l1的距离是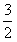 ,求点M的坐标。
,求点M的坐标。 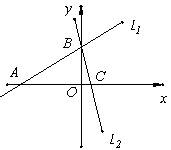

把一边长为40cm的正方形硬纸板,进行适当的剪裁,折成一个长方形盒子(纸板的厚度忽略不计)。
(1)如图1,若在正方形硬纸板的四角各剪一个同样大小的正方形,将剩余部分折成一个无盖的长方形盒子。
①要使折成的长方形盒子的底面积为484cm2,那么剪掉的正方形的边长为多少?
②折成的长方形盒子的侧面积是否有最大值?如果有,求出这个最大值及此时剪掉的正方形的边长;如果没有,请说明理由。
(2)如图2在正方形硬纸板上剪掉一些矩形(图2中阴影为剪去部分),将剩余部分折成一个有盖的长方形盒子,若折成的一个长方形盒子的表面积为550cm2,求此时长方形盒子的长、宽、高。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com