（本小题满分8分）列方程解应用题：

现加工一批机器零件，甲单独完成需4天，乙单独完成需6天。现由乙先做1天，然后两人合做，完成后共得报酬600元。若按个人完成的工作量给付报酬，你应如何分配呢？

（本小题满分8分） 已知下列n(n为正整数)个关于x的一元二次方程:

①② ③（n）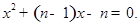

⑴请解上述一元二次方程①、②、③、（n）;

⑵请你指出这n 个方程的根具有什么共同特点，写出一条即可。

（本小题满分10分）

数形结合作为一种数学思想方法，数形结合的应用大致又可分为两种情形：或者借助于数的精确性来阐明形的某些属性，即“以数解形”；或者借助形的几何直观性来阐明数之间的某种关系，即 “以形助数”。                                                            

如浙教版九上课本第109页作业题第2题：如图1，已知在△ABC中，∠ACB=900，CD⊥AB，D为垂足。易证得两个结论：(1)AC·BC = AB·CD   (2)AC2= AD·AB

（1）请你用数形结合的“以数解形”思想来解：如图2，已知在△ABC中（AC>BC），∠ACB=900，CD⊥AB，D为垂足， CM平分∠ACB,且BC、AC是方程x2-14x+48=0的两个根，求AD、MD的长。

（2）请你用数形结合的“以形助数”思想来解： 设a、b、c、d都是正数，满足a：b=c：d,且a最大。求证：a+d>b+c（提示：不访设AB=a,CD=d,AC=b,BC=c，构造图1）

（本小题满分12分）

如图（1）在Rt△ACB中，∠C=90°AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动，速度为1 cm／s；点Q由A出发沿AC方向向点C匀速运动，速度为2cm／s;连接PQ。若设运动的时间为t(s)(0＜t＜2).根据以上信息，解答下列问题：

（1）当t为何值时，以A、P、Q为顶点的三角形与△ABC相似？

（2）设四边形PQCB的面积为y（），直接写出y与t之间的函数关系式；

（3）在点P、点Q的移动过程中，如果将△APQ沿其一边所在直线翻折，翻折后的三角形与△APQ组成一个四边形，那么是否存在某一时刻t，使组成的四边形为菱形？若存在，求出t的值；若不存在，请说明理由.

图（1）                 备用图                 备用图

（本小题满分8分）列方程解应用题：

现加工一批机器零件，甲单独完成需4天，乙单独完成需6天。现由乙先做1天，然后两人合做，完成后共得报酬600元。若按个人完成的工作量给付报酬，你应如何分配呢？