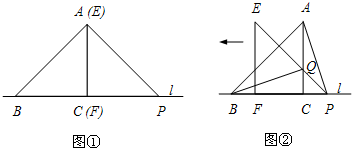如图①，将两块全等的直角三角形纸板摆放在坐标系中，已知BC=4，AC=5．
（1）求点A坐标和直线AC的解析式；
（2）折三角形纸板ABC，使边AB落在边AC上，设折痕交BC边于点E（图②），求点E坐标；
（3）将三角形纸板ABC沿AC边翻折，翻折后记为△AMC，设MC与AD交于点N，请在图③中画出图形，并求出点N坐标．

阅读：如图1把两块全等的含45°的直角三角板ABC和DEF叠放在一起，使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合，把三角板ABC固定不动，让三角板DEF绕点D旋转，两边分别与线段AB、BC相交于点P、Q，易说明△APD∽△CDQ．
猜想（1）：如图2，将含30°的三角板DEF（其中∠EDF=30°）的锐角顶点D与等腰三角形ABC（其中∠ABC=120°）的底边中点O重合，两边分别与线段AB、BC相交于点P、Q．写出图中的相似三角形（直接填在横线上）；
验证（2）：其它条件不变，将三角板DEF旋转至两边分别与线段AB的延长线、边BC相交于点P、Q．上述结论还成立吗？请你在图3上补全图形，并说明理由．
连接PQ，△APD与△DPQ是否相似？为什么？
探究（3）：根据（1）（2）的解答过程，你能将两三角板改为一个更为一般的条件，使得（1）成立？