
题目列表(包括答案和解析)
在△ABC中,∠A,∠B,∠C所对的边分别用a,b,c表示.
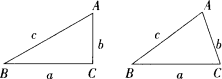
(1)如图,在△ABC中,∠A=2∠B,且∠A=60°.求证:a2=b(b+c);
(2)如果一个三角形的一个内角等于另一个内角的2倍,我们称这样的三角形为“倍角三角形”.本题第一问中的三角形是一个特殊的倍角三角形,那么对于任意的倍角三角形ABC,其中∠A=2∠B,关系式a2=b(b+c)是否仍然成立?请证明你的结论.
 ,b=1,c=2.求证:△ABC为倍角三角形﹔
,b=1,c=2.求证:△ABC为倍角三角形﹔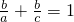 .
.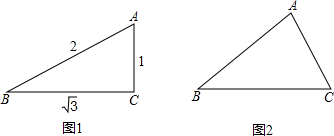
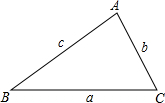 我们给出如下定义:如果一个三角形的一个内角等于另一个内角的2倍,我们称这样的三角形为“倍角三角形”.在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c.
我们给出如下定义:如果一个三角形的一个内角等于另一个内角的2倍,我们称这样的三角形为“倍角三角形”.在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c.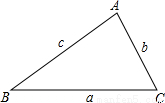
| 3 |
| b |
| a |
| b |
| c |

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com