
题目列表(包括答案和解析)
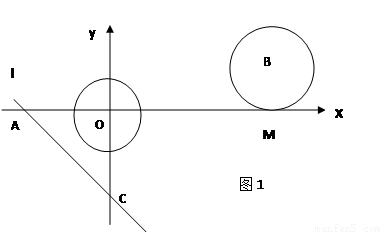
如图1,在平面直角坐标系中,以坐标原点O为圆心的⊙O的半径为![]() -1,直线l y=-X-
-1,直线l y=-X-![]() 与坐标轴分别交于A,C两点,点B的坐标为(4,1) ,⊙B与X轴相切于点M.
与坐标轴分别交于A,C两点,点B的坐标为(4,1) ,⊙B与X轴相切于点M.
(1) 求点A的坐标及∠CAO的度数;
(2) ⊙B以每秒1个单位长度的速度沿X轴负方向平移,同时,直线l绕点A顺时针匀速旋转.当⊙B第一次与⊙O相切时,直线l也恰好与⊙B第一次相切.问:直线AC绕点A每秒旋转多少度?
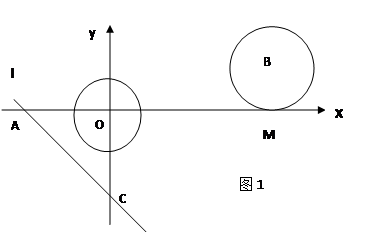
(3)如图2.过A,O,C三点作⊙O1,点E是劣弧![]() 上一点,连接EC,EA.EO,当点E在劣弧
上一点,连接EC,EA.EO,当点E在劣弧![]() 上运动时(不与A,O两点重合),
上运动时(不与A,O两点重合),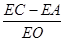 的值是否发生变化?如果不变,求其值,如果变化,说明理由.
的值是否发生变化?如果不变,求其值,如果变化,说明理由.
 .
.
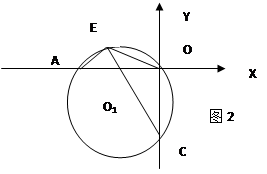
【解析】(1)已知点A,C的坐标,故可推出OA=OC,最后可得∠CAO=45°.
(2)依题意,设⊙B平移t秒到⊙B1处与⊙O第一次相切,连接B1O,B1N,则MN=3.连接B1A,B1P可推出∠PAB1=∠NAB1.又因为OA=OB1=![]() ,故∠AB1O=∠NAB1,∠PAB1=∠AB1O继而推出PA∥B1O.然后在Rt△NOB1中∠B1ON=45°,∴∠PAN=45°得出∠1=90°.然后可得直线AC绕点A平均每秒30度.
,故∠AB1O=∠NAB1,∠PAB1=∠AB1O继而推出PA∥B1O.然后在Rt△NOB1中∠B1ON=45°,∴∠PAN=45°得出∠1=90°.然后可得直线AC绕点A平均每秒30度.
(3)在CE上截取CK=EA,连接OK,证明△OAE≌△OCK推出OE=OK,∠EOA=∠KOC,∠EOK=∠AOC=90°.最后可证明![]()
如图1,在平面直角坐标系中,以坐标原点O为圆心的⊙O的半径为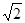 -1,直线l y=-X-
-1,直线l y=-X-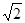 与坐标轴分别交于A,C两点,点B的坐标为(4,1) ,⊙B与X轴相切于点M.
与坐标轴分别交于A,C两点,点B的坐标为(4,1) ,⊙B与X轴相切于点M.
(1) 求点A的坐标及∠CAO的度数;
(2) ⊙B以每秒1个单位长度的速度沿X轴负方向平移,同时,直线l绕点A顺时针匀速旋转.当⊙B第一次与⊙O相切时,直线l也恰好与⊙B第一次相切.问:直线AC绕点A每秒旋转多少度?
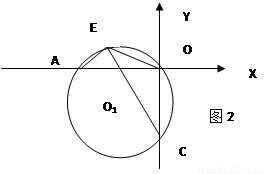
(3)如图2.过A,O,C三点作⊙O1
,点E是劣弧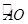 上一点,连接EC,EA.EO,当点E在劣弧
上一点,连接EC,EA.EO,当点E在劣弧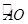 上运动时(不与A,O两点重合),
上运动时(不与A,O两点重合),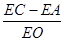 的值是否发生变化?如果不变,求其值,如果变化,说明理由.
的值是否发生变化?如果不变,求其值,如果变化,说明理由.
 .
.
【解析】(1)已知点A,C的坐标,故可推出OA=OC,最后可得∠CAO=45°.
(2)依题意,设⊙B平移t秒到⊙B1处与⊙O第一次相切,连接B1O,B1N,则MN=3.连接B1A,B1P可推出∠PAB1=∠NAB1.又因为OA=OB1=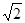 ,故∠AB1O=∠NAB1,∠PAB1=∠AB1O继而推出PA∥B1O.然后在Rt△NOB1中∠B1ON=45°,∴∠PAN=45°得出∠1=90°.然后可得直线AC绕点A平均每秒30度.
,故∠AB1O=∠NAB1,∠PAB1=∠AB1O继而推出PA∥B1O.然后在Rt△NOB1中∠B1ON=45°,∴∠PAN=45°得出∠1=90°.然后可得直线AC绕点A平均每秒30度.
(3)在CE上截取CK=EA,连接OK,证明△OAE≌△OCK推出OE=OK,∠EOA=∠KOC,∠EOK=∠AOC=90°.最后可证明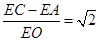
如图,抛物线![]() 交
交![]() 轴于A、B两点(A点在B点左侧),交
轴于A、B两点(A点在B点左侧),交![]() 轴于点C,已知B(8,0),
轴于点C,已知B(8,0),![]() ,△ABC的面积为8.
,△ABC的面积为8.
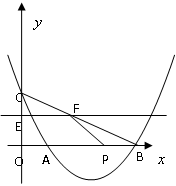
1.求抛物线的解析式;
2.若动直线EF(EF∥![]() 轴)从点C开始,以每秒1个长度单位的速度沿
轴)从点C开始,以每秒1个长度单位的速度沿![]() 轴负方向平移,且交
轴负方向平移,且交![]() 轴、线段BC于E、F两点,动点P同时从点B出发,在线段OB上以每秒2个单位的速度向原点O运动。连结FP,设运动时间
轴、线段BC于E、F两点,动点P同时从点B出发,在线段OB上以每秒2个单位的速度向原点O运动。连结FP,设运动时间![]() 秒。当
秒。当![]() 为何值时,
为何值时,![]() 的值最大,并求出最大值;
的值最大,并求出最大值;
3.在满足(2)的条件下,是否存在![]() 的值,使以P、B、F为顶点的三角形与△ABC相似。若存在,试求出
的值,使以P、B、F为顶点的三角形与△ABC相似。若存在,试求出![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
如图,抛物线![]() 交
交![]() 轴于A、B两点(A点在B点左侧),交
轴于A、B两点(A点在B点左侧),交![]() 轴于点C,已知B(8,0),
轴于点C,已知B(8,0),![]() ,△ABC的面积为8.
,△ABC的面积为8.
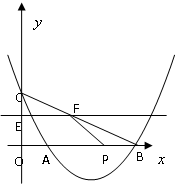
1.求抛物线的解析式;
2.若动直线EF(EF∥![]() 轴)从点C开始,以每秒1个长度单位的速度沿
轴)从点C开始,以每秒1个长度单位的速度沿![]() 轴负方向平移,且交
轴负方向平移,且交![]() 轴、线段BC于E、F两点,动点P同时从点B出发,在线段OB上以每秒2个单位的速度向原点O运动。连结FP,设运动时间
轴、线段BC于E、F两点,动点P同时从点B出发,在线段OB上以每秒2个单位的速度向原点O运动。连结FP,设运动时间![]() 秒。当
秒。当![]() 为何值时,
为何值时,![]() 的值最大,并求出最大值;
的值最大,并求出最大值;
3.在满足(2)的条件下,是否存在![]() 的值,使以P、B、F为顶点的三角形与△ABC相似。若存在,试求出
的值,使以P、B、F为顶点的三角形与△ABC相似。若存在,试求出![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
如图,抛物线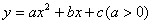 交
交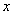 轴于A、B两点(A点在B点左侧),交
轴于A、B两点(A点在B点左侧),交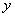 轴于点C,已知B(8,0),
轴于点C,已知B(8,0),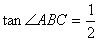 ,△ABC的面积为8.
,△ABC的面积为8.

1.求抛物线的解析式;
2.若动直线EF(EF∥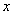 轴)从点C开始,以每秒1个长度单位的速度沿
轴)从点C开始,以每秒1个长度单位的速度沿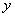 轴负方向平移,且交
轴负方向平移,且交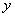 轴、线段BC于E、F两点,动点P同时从点B出发,在线段OB上以每秒2个单位的速度向原点O运动。连结FP,设运动时间
轴、线段BC于E、F两点,动点P同时从点B出发,在线段OB上以每秒2个单位的速度向原点O运动。连结FP,设运动时间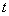 秒。当
秒。当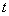 为何值时,
为何值时,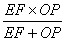 的值最大,并求出最大值;
的值最大,并求出最大值;
3.在满足(2)的条件下,是否存在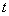 的值,使以P、B、F为顶点的三角形与△ABC相似。若存在,试求出
的值,使以P、B、F为顶点的三角形与△ABC相似。若存在,试求出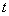 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com