
题目列表(包括答案和解析)
(1)∵CE∥BF,
∴∠DBF=∠DCE, ……………………………………2分
∵D是BC的中点,
∴BD=CD,
又∠BDF=∠CDE,
∴△BDF≌△CDE. ……………………………………5分
(2)由(1)知,△BDF≌△CDE.
∴CE=BF, …………………………………6分
∵CE∥BF,
∴四边形BFCE是平行四边形. …………………………8分
在△ABC中,∵AB=AC,BD=CD,
∴AD⊥BC,即EF⊥BC,
∴四边形BFCE是菱形, ……………………………………10分
(本题满分6分)在△ABC中,∠C=90°,DE垂直平分斜边AB,分别交AB、BC于D、E,若∠CAE=∠B+30°,求∠AEC的度数。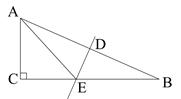
(本题满分8分)
在△ABC中,AB=CB,∠ABC=90º,F为AB延长线上一点,点E在BC上,且AE=CF.

1.(1)求证: Rt△ABE≌Rt△CBF;
2.(2)若∠CAE=30º,求∠ACF度数.
(本题满分10分)如图1,在△ABC中,AB=BC=5,AC="6." △ECD是△ABC沿BC方向平移得到的,连接AE.AC和BE相交于点O.
(1)判断四边形ABCE是怎样的四边形,说明理由;
(2)如图2,P是线段BC上一动点(图2),(不与点B、C重合),连接PO并延长交线段AE于点Q,QR⊥BD,垂足为点R.
①四边形PQED的面积是否随点P的运动而发生变化?
若变化,请说明理由;若不变,求出四边形PQED的面积;
②当线段BP的长为何值时,△PQR与△BOC相似?
(本题满分10分,其中每小题各5分)
已知:如图,在△ABC中,AB=6,BC=8,∠B=60°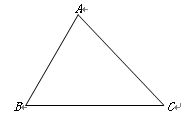
求:【小题1】(1)△ABC的面积;
【小题2】(2)∠C的余弦值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com