
题目列表(包括答案和解析)
(本小题共13分)
数列![]() 满足
满足![]() ,
,![]() (
(![]() ),
),![]() 是常数。
是常数。
(Ⅰ)当![]() 时,求
时,求![]() 及
及![]() 的值;
的值;
(Ⅱ)数列![]() 是否可能为等差数列?若可能,求出它的通项公式;若不可能,说明理由;
是否可能为等差数列?若可能,求出它的通项公式;若不可能,说明理由;
(Ⅲ)求![]() 的取值范围,使得存在正整数
的取值范围,使得存在正整数![]() ,当
,当![]() 时总有
时总有![]() 。
。
(本小题共13分)
数列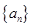 满足
满足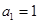 ,
, (
(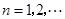 ),
), 是常数。
是常数。
(Ⅰ)当 时,求
时,求 及
及 的值;
的值;
(Ⅱ)数列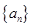 是否可能为等差数列?若可能,求出它的通项公式;若不可能,说明理由;
是否可能为等差数列?若可能,求出它的通项公式;若不可能,说明理由;
(Ⅲ)求 的取值范围,使得存在正整数
的取值范围,使得存在正整数 ,当
,当 时总有
时总有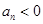 。
。
((本小题共13分)
若数列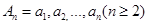 满足
满足 ,数列
,数列 为
为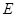 数列,记
数列,记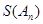 =
= .
.
(Ⅰ)写出一个满足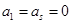 ,且
,且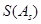 〉0的
〉0的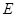 数列
数列 ;
;
(Ⅱ)若 ,n=2000,证明:E数列
,n=2000,证明:E数列 是递增数列的充要条件是
是递增数列的充要条件是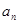 =2011;
=2011;
(Ⅲ)对任意给定的整数n(n≥2),是否存在首项为0的E数列 ,使得
,使得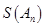 =0?如果存在,写出一个满足条件的E数列
=0?如果存在,写出一个满足条件的E数列 ;如果不存在,说明理由。
;如果不存在,说明理由。
【解析】:(Ⅰ)0,1,2,1,0是一具满足条件的E数列A5。
(答案不唯一,0,1,0,1,0也是一个满足条件的E的数列A5)
(Ⅱ)必要性:因为E数列A5是递增数列,所以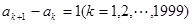 .所以A5是首项为12,公差为1的等差数列.所以a2000=12+(2000—1)×1=2011.充分性,由于a2000—a1000
.所以A5是首项为12,公差为1的等差数列.所以a2000=12+(2000—1)×1=2011.充分性,由于a2000—a1000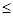 1,a2000—a1000
1,a2000—a1000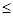 1……a2—a1
1……a2—a1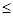 1所以a2000—a
1所以a2000—a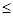 19999,即a2000
19999,即a2000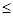 a1+1999.又因为a1=12,a2000=2011,所以a2000=a1+1999.故
a1+1999.又因为a1=12,a2000=2011,所以a2000=a1+1999.故 是递增数列.综上,结论得证。
是递增数列.综上,结论得证。
((本小题共13分)
若数列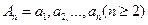 满足
满足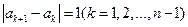 ,数列
,数列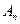 为
为 数列,记
数列,记 =
=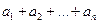 .
.
(Ⅰ)写出一个满足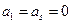 ,且
,且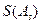 〉0的
〉0的 数列
数列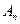 ;
;
(Ⅱ)若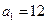 ,n=2000,证明:E数列
,n=2000,证明:E数列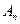 是递增数列的充要条件是
是递增数列的充要条件是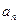 =2011;
=2011;
(Ⅲ)对任意给定的整数n(n≥2),是否存在首项为0的E数列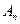 ,使得
,使得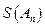 =0?如果存在,写出一个满足条件的E数列
=0?如果存在,写出一个满足条件的E数列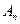 ;如果不存在,说明理由。
;如果不存在,说明理由。
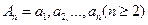 满足
满足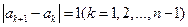 ,数列
,数列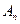 为
为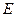 数列,记
数列,记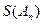 =
=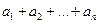 .
.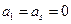 ,且
,且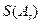 〉0的
〉0的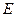 数列
数列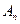 ;
;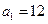 ,n=2000,证明:E数列
,n=2000,证明:E数列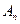 是递增数列的充要条件是
是递增数列的充要条件是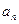 =2011;
=2011;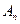 ,使得
,使得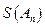 =0?如果存在,写出一个满足条件的E数列
=0?如果存在,写出一个满足条件的E数列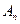 ;如果不存在,说明理由。
;如果不存在,说明理由。湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com