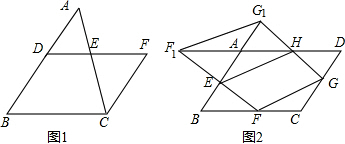
操作1:如图1,一三角形纸片ABC,分别取AB、AC的中点D、E,连接DE,沿DE将纸片剪开,并将其中的△ADE纸片绕点E旋转180°后可拼合(无重叠无缝隙)成平行四边形纸片BCFD.
操作2:如图2,一平行四边形纸片ABCD,E、F、G、H分别是AB、BC、CD、AD边的中点,沿EF剪开并将其中的△BFE纸片绕点E旋转180°到△AF
1E位置;沿HG剪开并将其中的△DGH纸片绕点H旋转180°到△AG
1H位置;沿FG剪开并将△CFG纸片放置于△AF
1G
1的位置,此时四张纸片恰好拼合(无重叠无缝隙)成四边形FF
1G
1G.则四边形FF
1G
1G的形状是
.
操作、思考并探究:
(1)如图3,如果四边形ABCD是任意四边形(不是梯形或平行四边形)的纸片,E、F、G、H分别是AB、BC、CD、AD的中点.依次沿EF、FG、GH、HE剪开得到四边形纸片EFGH.请判断四边形纸片EFGH的形状,并说明理由.
(2)你能将上述四边形纸片ABCD经过恰当地剪切后拼合(无重叠无缝隙)成一个平行四边形纸片?请在图4上画出对应的示意图.

(3)如图5,E、F、G、H分别是四边形ABCD各边的中点,若△AEH、△BEF、△CFG、△DGH的面积分别为S
1、S
2、S
3、S
4,且S
1=2,S
3=5,则四边形ABCD是面积是
.(不要求说明理由)

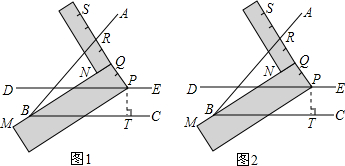 (1)阅读理解:
(1)阅读理解: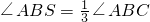 是否成立?如果成立,请说明理由;如果不成立,请在图2中∠ABC的外部画出
是否成立?如果成立,请说明理由;如果不成立,请在图2中∠ABC的外部画出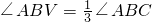 (无需写画法,保留画图痕迹即可).
(无需写画法,保留画图痕迹即可).




