
题目列表(包括答案和解析)
| p |
| q |
| 1 |
| 3 |
 第
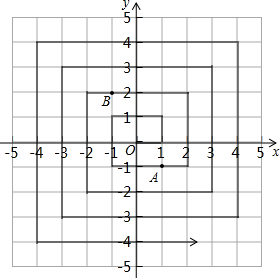
第 (p是整数,q是正整数),它可以对应网格纸(如图)上的一个点,即p所在行与q所在列的交点,记为(q,p).如
(p是整数,q是正整数),它可以对应网格纸(如图)上的一个点,即p所在行与q所在列的交点,记为(q,p).如 对应图中的点A(3,1),这样,每个有理数对应着网格纸上的格点(水平线与竖直线的交叉点),而康托尔用图中的方法从中心O出发“螺旋式”地扩展开去,将平面内所有格点“一网打尽”.在图中,O(0,0)是第一个点,A(1,-1)是第________个点,B(-1,2)是
对应图中的点A(3,1),这样,每个有理数对应着网格纸上的格点(水平线与竖直线的交叉点),而康托尔用图中的方法从中心O出发“螺旋式”地扩展开去,将平面内所有格点“一网打尽”.在图中,O(0,0)是第一个点,A(1,-1)是第________个点,B(-1,2)是 第________个点,第35个点是________.
第________个点,第35个点是________.阅读下列材料,并回答后面的问题。
我们知道分数![]() 写成小数形式即0.
写成小数形式即0.![]() ,反过来,无限循环小数0.
,反过来,无限循环小数0.![]() 写成分数形式即
写成分数形式即![]() 。一般的,任何一个循环小数都可以写成为分数。以0.
。一般的,任何一个循环小数都可以写成为分数。以0.![]() 为例,先设0.
为例,先设0.![]() =x,由0.
=x,由0.![]() = 0.777…可知,10x=7.777…,所以10x-x=7,解方程,得x=
= 0.777…可知,10x=7.777…,所以10x-x=7,解方程,得x=![]()
(1) 想一想,如何把无限循环小数0.![]()
![]() 化成分数?请动手试一试。
化成分数?请动手试一试。
(2) 下列小数可写成什么分数?请直接写出。
0.![]()
![]() = 0.
= 0.![]()
![]()
![]() =
=
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com