（本小题满分10分）

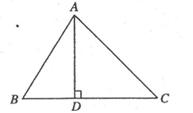
（1）如图24—1，已知△ABC中，∠BAC＝45°，AB="AC," AD⊥BC于D， 将△ABC沿AD剪开，并分别以AB、AC为轴翻转，点E、F分别是点D的对应点，得到△ABE和△ACF (与△ABC在同一平面内)．延长EB、FC相交于G点，证明四边形AEGF是正方形；
（2）如果⑴中AB≠AC，其他不变，如图24—2．那么四边形AEGF是否是正方形？请说明理由．
（3）在⑵中，若BD＝2，DC＝3，求AD的长．

小明和同桌小聪在课后做作业时，对课本中的一道作业题，进行了认真探索。

【作业题】如图1，一个半径为100m的圆形人工湖如图所示，弦AB是湖上的一座桥，测得圆周角∠C=45°,求桥AB的长。

小明和小聪经过交流，得到了如下的两种解决方法：

方法一：延长BO交⊙O与点E，连接AE，得 Rt△ABE，∠E=∠C，∴AB=100；

方法二：作AB的弦心距OH，连接OB, ∴∠BOH=∠C，解Rt△OHB, ∴HB=50，

∴AB=100。

感悟：圆内接三角形的一边和这边的对锐角、圆的半径(或直径)这三者关系，

可构成直角三角形，从而把一边和这边的对锐角﹑半径建立一个关系式。

（1）问题解决：受到(1)的启发，请你解下面命题：如图2，点A（3，0）、B（0，），C为直线AB上一点，过A、O、C的⊙E的半径为2. 求线段OC的长。

（2）问题拓展：如图3，△ABC中，∠ ACB=75°，∠ABC=45°，AB=2，D是线段BC上的一个动点，以AD为直径画⊙O分别交AB，AC于E，F，连结EF, 设⊙O半径为x, EF为y.

①     y关于x的函数关系式；②求线段EF长度的最小值。

观察与思考：阅读下列材料，并解决后面的问题
在锐角△ABC中，∠A、∠B、∠C的对边分别是a、b、c，过A作AD⊥BC于D（如图（1）），则，即AD=csinB，AD=bsinC，于是csinB=bsinC，即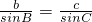，同理有：，
所以．
即：在一个三角形中，各边和它所对角的正弦的比相等在锐角三角形中，若已知三个元素（至少有一条边），运用上述结论和有关定理就可以求出其余三个未知元素．
根据上述材料，完成下列各题．

（1）如图（2），△ABC中，∠B=45°，∠C=75°，BC=60，则∠A=______；AC=______；
（2）自从去年日本政府自主自导“钓鱼岛国有化”闹剧以来，我国政府灵活应对，现如今已对钓鱼岛执行常态化巡逻．某次巡逻中，如图（3），我渔政204船在C处测得A在我渔政船的北偏西30°的方向上，随后以40海里/时的速度按北偏东30°的方向航行，半小时后到达B处，此时又测得钓鱼岛A在的北偏西75°的方向上，求此时渔政204船距钓鱼岛A的距离AB．（结果精确到0.01，）

如果三角形有一边上的中线长恰好等于这边的长，那么称这个三角形为“好玩三角形”

（1）请用直尺与圆规画一个“好玩三角形”；

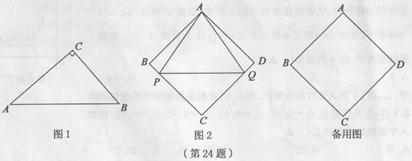
（2）如图1，在Rt⊿ABC中，∠C=90°，，求证：⊿ABC是“好玩三角形”；

（3）如图2，已知菱形ABCD的边长为a, ∠ABC=2β，点P，Q从点A同时出发，以相同的速度分别沿折线AB-BC和AD-DC向终点C运动，记点P所经过的路程为S

①当β=45°时，若⊿APQ是“好玩三角形”，试求的值

②当tanβ的取值在什么范围内，点P，Q在运动过程中，有且只有一个⊿APQ能成为“好玩三角形”请直接写出tanβ的取值范围。

（4）本小题为选做题

依据（3）中的条件，提出一个关于“在点P，Q的运动过程中，tanβ的取值范围与⊿APQ是“好玩三角形”的个数关系的真命题（“好玩三角形”的个数限定不能为1）。