练习册

  • 练习册
  • 试题
    如图所示.已知正四棱柱ABCD-A1B1C1D1.点E在棱D1D上.截面EAC∥D1B.且面EAC与底面ABCD所成的角为450.AB＝a. 【查看更多】

     

    题目列表(包括答案和解析)

    （本小题满分12分）如图所示，已知圆
     
    为圆上一动点，点P在AM上，点N在CM上，且满

    足的轨迹为曲线E.

    （1）求曲线E的方程；（II）若过定点F（0，2）

    的直线交曲线E于不同的两点G、H（点G在点F、H之间），

    且满足，求的取值范围.

    查看答案和解析>>

    （本小题满分12分）

    如图所示，已知S是正三角形ABC所在平面外的一点，且SA=SB=SC，SG为△SAB上的高，D、E、F分别是AC、BC、SC的中点，试判断SG与平面DEF的位置关系，并给予证明.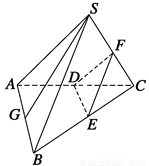

     

    查看答案和解析>>

    （本小题满分12分）如图所示，已知六棱锥的底面是正六边形，平面，是的中点。

    （Ⅰ）求证：平面//平面；

    （Ⅱ）设，当二面角的大小为时，求的值。

     

    查看答案和解析>>

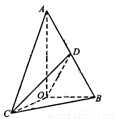
    （本小题满分12分）如图所示，已知中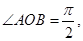，AB=2OB=4，D为AB的中点，若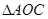是绕直线AO旋转而成的，记二面角B—AO—C的大小为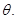（I）若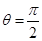，求证：平面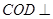平面AOB；（II）若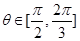时，求二面角C—OD—B的余弦值的最小值。

     

     

     

     

     

     

    查看答案和解析>>

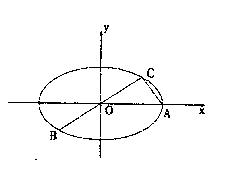
    （本小题满分12分）如图所示，已知A、B、C是椭圆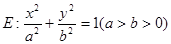上三点，其中点A的坐标为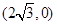，BC过椭圆的中心O，且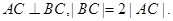

       （Ⅰ）求点C的坐标及椭圆E的方程；

       （Ⅱ）若椭圆E上存在两点P， Q，使得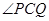的平分线总垂直于z轴，试判断向量是否共线，并给出证明．

                           

     

    查看答案和解析>>

     

    一、DCABB   DDCBC   AB

    二、13.  192    14.   ―640     15.   4     16.   

    17.

    （1）     …5分

    （2）由已知及（1）知     

    学科网(Zxxk.Com)由学科网(Zxxk.Com)正弦定理得：

       ……………………10分

    18.由题设及等比数列的性质得  ①

    又                 ②

    由①②得  或            …………………4分

        或                     …………………6分

    或                      …………………8分

    当时，        …………………10分

    当时，………………12分

    19.略（见课本B例1）

    20.解：

    （1）在正四棱柱中，因为

    所以           

    又             

    连接交于点，连接，则，所以

    所以是由截面与底面所成二面角的平面角，即

    学科网(Zxxk.Com)

    所以                 .....................4分

    （2）由题设知是正四棱柱.

    因为                  

    所以                   

    又                     

    所以是异面直线与之间的距离。

    因为，而是截面与平面的交线，

    所以                     

                       

    即异面直线与之间的距离为

    （3）由题知

                            

    因为                    

    所以是三棱锥的高，

    在正方形中，分别是的中点，则

                                 

    所以                    

    即三棱锥的体积是.

    21.(1)解：，由此得切线的方程为

             ………………………4分

    (2)切线方程令，得

    ①

    当且仅当时等号成立。………………………9分

    ②若，则又由

                       ………………………12分

    22.（1）由题可得，设  

     

      

    又   又

        点P的坐标为   ……………………3分

     

    （2）由题意知，量直线的斜率必存在，设PB的斜率为

    则PB的直线方程为：由  得

    ,显然1是该方程的根

    ,依题意设故可得A点的横坐标

     

                       ……………………7分

    （3）设AB的方程为，带入并整理得

                   

                      

       …………………（）

    设

                     

    点P到直线AB的距离

    当且仅当，即时取“=”号（满足条件）

    故的面积的最大值为2                      ………………………12分

     

     

     

     


    同步练习册答案