阅读理解题：
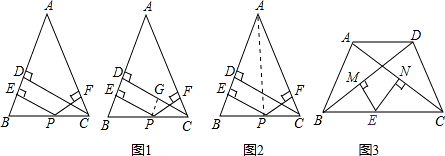
已知：如图，△ABC中，AB=AC，P是底边BC上的任一点（不与B、C重合），CD⊥AB于D，PE⊥AB于E，PF⊥AC于F．
求证：CD=PE+PF．
在解答这个问题时，小明与小颖的思路方法分别如下：
小明的思路方法是：过点P作PG⊥CD于G（如图1），则可证得四边形PEDG是矩形，也可证得△PCG≌△CPF，从而得到PE=DG，PF=CG，因此得CD=PE+PF．
小颖的思路方法是：连接PA（如图2），则S_△ABC=S_△PAB+S_△PAC，再由三角形的面积公式便可证得CD=PE+PF．
由此得到结论：等腰三角形底边上任意一点到两腰的距离之和等于一腰上的高．
阅读上面的材料，然后解答下面的问题：
（1）针对小明或小颖的思路方法，请选择俩人中的一种方法把证明过程补充完整
（2）如图3，梯形ABCD中，AD∥BC，∠ABC=60°，AB=AD=CD=2，E是BC上任意一点，EM⊥BD于M，EN⊥AC于N，试利用上述结论
求EM+EN的值．