
题目列表(包括答案和解析)

| 9 | 2 |
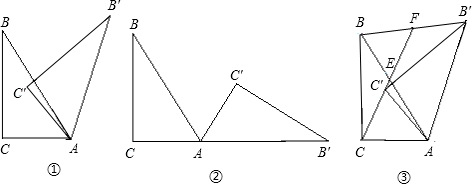
如图①,△ABC中,,∠ABC=
,将△ABC绕点A顺时针旋转得到△AB ¢C ¢ ,设旋转的角度是
.
(1)如图②,当= °(用含
的代数式表示)时,点B ¢恰好落在CA的延长线上;
(2)如图③,连结BB ¢ 、CC ¢, CC ¢ 的延长线交斜边AB于点E,交BB ¢于点F.请写出图中两对相似三角形 ,
(不含全等三角形),并选一对证明.
 ,∠ABC=
,∠ABC= ,将△ABC绕点A顺时针旋转得到△AB ¢C ¢,设旋转的角度是
,将△ABC绕点A顺时针旋转得到△AB ¢C ¢,设旋转的角度是 .
.


 =" " °(用含
=" " °(用含 的代数式表示)时,点B ¢恰好落在CA的延长线上;
的代数式表示)时,点B ¢恰好落在CA的延长线上;湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com