
题目列表(包括答案和解析)
| 2 |
| 1 |
| 3 |
| 2 |
| x+2 |
| x-6 |
| x2-4 |
| 2(x-2) |
| (x+2)(x-2) |
| x-6 |
| (x+2)(x-2) |
| 1 |
| x-2 |
| 1 |
| x-2 |


|
|
|
|
|
|
|
(11·佛山)现在初中课本里所学习的概率计算问题只有以下类型:
第一类是可以列举有限个等可能发生的结果的概率计算问题(一步试验直接列举,两步以上的试验可以借助树状图或表格列举),比如掷一枚均匀硬币的试验;
第二类是用试验或者模拟试验的数据计算频率,并用频率估计概率的概率计算问题,比如掷图钉的试验;
解决概率计算问题,可以直接利用模型,也可以转化后再利用模型;
请解决以下问题
(1)如图,类似课本的一个寻宝游戏,若宝物随机藏在某一块砖下(图中每一块砖除颜色外完全相同),则宝物藏在阴影砖下的概率是多少?
(2)在![]() 中随机选取3个整数,若以这3个整数为边长构成三角形的情况如下表:
中随机选取3个整数,若以这3个整数为边长构成三角形的情况如下表:
请你根据表中数据,估计构成钝角三角形的概率是多少?(精确到百分位)
(11·佛山)现在初中课本里所学习的概率计算问题只有以下类型:
第一类是可以列举有限个等可能发生的结果的概率计算问题(一步试验直接列举,两步以上的试验可以借助树状图或表格列举),比如掷一枚均匀硬币的试验;
第二类是用试验或者模拟试验的数据计算频率,并用频率估计概率的概率计算问题,比如掷图钉的试验;
解决概率计算问题,可以直接利用模型,也可以转化后再利用模型;
请解决以下问题
(1)如图,类似课本的一个寻宝游戏,若宝物随机藏在某一块砖下(图中每一块砖除颜色外完全相同),则宝物藏在阴影砖下的概率是多少 ?
?
(2)在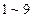 中随机选取3个整数,若以这3个整数为边长构成三角形的情况如下表:
中随机选取3个整数,若以这3个整数为边长构成三角形的情况如下表:
请你根据表中数据,估计构成钝角三角形的概率是多少?(精确到百分位)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com