8．如下图.由∠1＝∠2.BC＝DC.AC＝EC.得△ABC≌△EDC的根据是——青夏教育精英家教网—

8．如下图.由∠1＝∠2.BC＝DC.AC＝EC.得△ABC≌△EDC的根据是【查看更多】

题目列表(包括答案和解析)

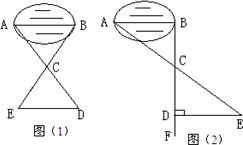
育才中学七年级(二)班学生到野外活动．为测量一池塘两端A、B的距离，设计了如下几种方案：(Ⅰ)如图A所示先在平地取一个可以直接到达A、B的点C，可连结AC、BC，并分别延长AC至D、BC至E，使DC＝AC，EC＝BC．最后测出DE的距离即为AB之长．(Ⅱ)(如图B所示)先过B点作AB的垂线BF，再在BF上取C、D两点，使BC＝CD．接着过点D作BD的垂线DE，交AC的延长线于E，则测出DE的长即为A、B的距离．

阅读后回答下列问题：

(1)方案(Ⅰ)是否可行？________，理由是________．

(2)方案(Ⅱ)是否切实可行？________，理由是________．

(3)方案(Ⅱ)中作BF⊥AB，ED⊥BF的目的是________；若仅满足∠ABD＝∠BDE≠90°，方案(Ⅱ)是否成立？________．

查看答案和解析>>

某校八年级(1)班学生到野外活动，为测量一池塘两端A、B的距离，设计出如下几种方案：

(Ⅰ)如图1，先在平地取一个可直接到达A、B的点C，再连接AC、BC，并分别延长AC至D，BC至E，使DC＝AC，EC＝BC，最后测出DE的距离即为AB之长．

(Ⅱ)如图2，先过B点作AB的垂线BF，再在BF上取C、D两点，使BC＝CD，接着过点D作BD的垂直线DE，交AC的延长线于E，则测出DE的长即为A、B的距离．

阅读后回答下列问题：

(1)

方案(Ⅰ)是否可行，理由是________．

(2)

方案(Ⅱ)是否可行，理由是________．

(3)

方案(Ⅱ)中作BD⊥AB，ED⊥BF的目的是________，若仅满足∠ABD＝∠BDE≠90°，方案(Ⅱ)，结论是否成立？

(4)

方案(Ⅱ)中，若使BC＝n·CD，能否测出(或求出)AB的长？理由是________，若ED＝________m，则AB＝________．

查看答案和解析>>

某班同学到野外活动，为测量一池塘两端A、B的距离，设计了几种方案，下面介绍两种：(Ⅰ)如图(1)，先在平地取一个可以直接到达A、B的点C，并分别延长AC到D，BC到E，使DC＝AC，BC＝EC，最后测出DE的距离即为AB的长．(Ⅱ)如图(2)，先过B点作AB的垂线BF，再在BF上取C、D两点，使BC＝CD，接着过点D作BD的垂线DE，交AC的延长线于E，则测出DE的长即为AB的距离．阅读后回答下列问题：