
题目列表(包括答案和解析)
| AF |
| BE |
| AF |
| BE |
| PQ |
| RS |
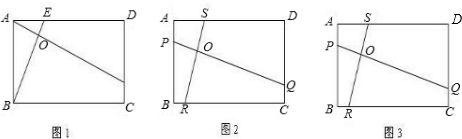
 的值;
的值; =k,通过变式,我们可以得到如下的两个命题:
=k,通过变式,我们可以得到如下的两个命题: =k;
=k;
如图1,矩形纸片ABCD的边长分别为a,b(a<b).将纸片任意翻折(如图2),折痕为PQ.(P在BC上),使顶点C落在四边形APCD内一点![]() ,
,![]() 的延长线交直线AD于M,再将纸片的另一部分翻折,使A落在直线PM上一点
的延长线交直线AD于M,再将纸片的另一部分翻折,使A落在直线PM上一点![]() ,且
,且![]() 所在直线与PM所在直线重合(如图3)折痕为MN.
所在直线与PM所在直线重合(如图3)折痕为MN.
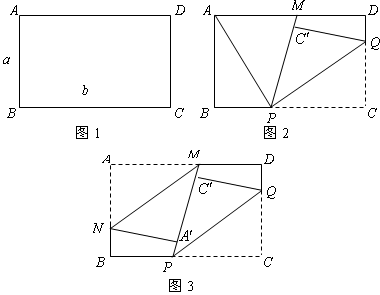
(1)猜想两折痕PQ,MN之间的位置关系,并加以证明.
(2)若∠QPC的角度在每次翻折的过程中保持不变,则每次翻折后,两折痕PQ,MN间的距离有何变化?请说明理由.
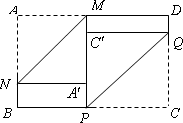
(3)若∠QPC的角度在每次翻折的过程中都为45°(如下图),每次翻折后,非重叠部分的四边形![]() ,及四边形
,及四边形![]() 的周长与a,b有何关系,为什么?
的周长与a,b有何关系,为什么?
已知:矩形纸片ABCD中,AB=26厘米,BC=18.5厘米,点E在AD上,且AE=6厘米,点P是![]() 边上一动点.按如下操作:
边上一动点.按如下操作:
步骤一,折叠纸片,使点P与点![]() 重合,展开纸片得折痕MN(如图23(1)所示);
重合,展开纸片得折痕MN(如图23(1)所示);
步骤二,过点P作![]() ,交MN所在的直线于点Q,连接QE(如图23(2)所示)
,交MN所在的直线于点Q,连接QE(如图23(2)所示)
(1)无论点P在![]() 边上任何位置,都有PQ QE(填“
边上任何位置,都有PQ QE(填“![]() ”、“
”、“![]() ”、“
”、“![]() ”号);
”号);
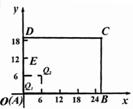
(2)如图23(3)所示,将纸片ABCD放在直角坐标系中,按上述步骤一、二进行操作:
①当点![]() 在
在![]() 点时,PT与MN交于点Q1 ,Q1点的坐标是( , );
点时,PT与MN交于点Q1 ,Q1点的坐标是( , );
②当PA=6厘米时,PT与MN交于点Q2 ,Q2点的坐标是( , );
③当PA=12厘米时,在图22(3)中画出MN,PT(不要求写画法),并求出MN与PT的交点Q3的坐标;
(3)点![]() 在运动过程中,PT与MN形成一系列的交点Q1 ,Q2 ,Q3 ,…观察、猜想:众多的交点形成的图象是什么?并直接写出该图象的函数表达式.
在运动过程中,PT与MN形成一系列的交点Q1 ,Q2 ,Q3 ,…观察、猜想:众多的交点形成的图象是什么?并直接写出该图象的函数表达式.
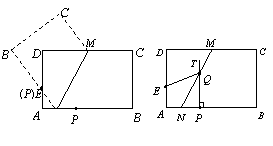 |
23(1) 23(2) 23(3)

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com