
题目列表(包括答案和解析)
阅读理解:对于任意正实数a,b,
![]() ,∴
,∴![]() ,∴a+b≥2
,∴a+b≥2![]() ,当且仅当a=b时,等号成立.
,当且仅当a=b时,等号成立.
结论:在a+b≥2![]() (a,b均为正实数)中,若ab为定值p,则
(a,b均为正实数)中,若ab为定值p,则![]() ,当且仅当a=b,a+b有最小值
,当且仅当a=b,a+b有最小值![]() .根据上述内容,回答下列问题:
.根据上述内容,回答下列问题:
(1)若x﹥0,只有当x= 时,![]() 有最小值 .
有最小值 .
(2)探索应用:如图,已知A(-2,0),B(0,-3),点P为双曲线![]() 上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
 |
| |
阅读理解:对于任意正实数a,b,![]() ,
,![]() ,
,
![]() ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.
结论:在![]() (a,b均为正实数)中,若ab为定值p,则
(a,b均为正实数)中,若ab为定值p,则![]() ,
,
只有当a=b时,a+b有最小值![]() .
.
根据上述内容,回答下列问题:
(1)若m>0,只有当m=________时,![]() 有最小值________.
有最小值________.
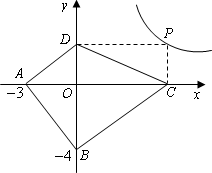
(2)探索应用:已知A(-3,0),B(0,-4),点P为双曲线![]() 上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于D.
上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于D.
求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
阅读理解:对于任意正实数a、b,∵![]() ≥0, ∴
≥0, ∴![]() ≥0,
≥0,
∴![]() ≥
≥![]() ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.
结论:在![]() ≥
≥![]() (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥![]() ,只有当a=b时,a+b有最小值
,只有当a=b时,a+b有最小值![]() .
.
根据上述内容,回答下列问题:
若m>0,只有当m= 时,![]() .
.
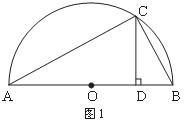
思考验证:如图1,AB为半圆O的直径,C为半圆上任意一点(与点A、B不重合)过点C作CD⊥AB,垂足为D,AD=a,DB=b.
试根据图形验证![]() ≥
≥![]() ,并指出等号成立时的条件.
,并指出等号成立时的条件.
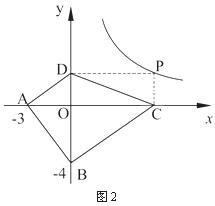
探索应用:如图2,已知A(-3,0),B(0,-4),P为双曲线![]() (x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
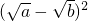 ≥0,∴a-
≥0,∴a- +b≥0,∴a+b≥2
+b≥0,∴a+b≥2 ,只有点a=b时,等号成立.
,只有点a=b时,等号成立. (a,b均为正实数)中,若ab为定值p,则a+b≥
(a,b均为正实数)中,若ab为定值p,则a+b≥ ,只有当a=b时,a+b有最小值2
,只有当a=b时,a+b有最小值2 .
. 有最小值;
有最小值; ,并指出等号成立时的条件;
,并指出等号成立时的条件; 上的任意一点,过点P作PC⊥x轴于点C,PO⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
上的任意一点,过点P作PC⊥x轴于点C,PO⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
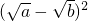 ≥0,∴a+b-2
≥0,∴a+b-2 ≥0,∴a+b≥2
≥0,∴a+b≥2 ,只有当a=b时,等号成立.
,只有当a=b时,等号成立. (a,b均为正实数)中,若ab为定值p,则a+b≥2
(a,b均为正实数)中,若ab为定值p,则a+b≥2 只有当a=b时,a+b有最小值2
只有当a=b时,a+b有最小值2 .
. 有最小值______.
有最小值______. (x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.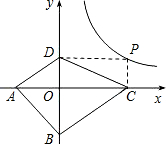
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com