
题目列表(包括答案和解析)
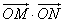 =0,其中点O为坐标原点.
=0,其中点O为坐标原点.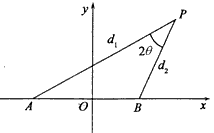
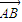 =
=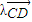 (实数λ≠0),证明:
(实数λ≠0),证明: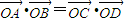 (O是坐标原点);
(O是坐标原点);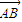 =
=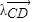 (实数λ≠0),证明:
(实数λ≠0),证明: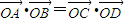 (O是坐标原点);
(O是坐标原点);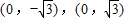 的距离之和为4,设点P的轨迹为C,直线y=kx+1与C交于A,B两点.
的距离之和为4,设点P的轨迹为C,直线y=kx+1与C交于A,B两点.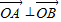 ,求k的值;
,求k的值;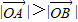 .
.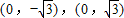 的距离之和为4,设点P的轨迹为C,直线y=kx+1与C交于A,B两点.
的距离之和为4,设点P的轨迹为C,直线y=kx+1与C交于A,B两点.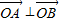 ,求k的值;
,求k的值; .
.一、选择题
1.C 2.B 3.B 4.D 5.B 6.C
7.D 8.C 9.C 10.C
二、填空题
11. 12.
12. 13.
13. 14.2 15.30°
14.2 15.30°
三、解答题
16.解:(Ⅰ)由 ,根据正弦定理得
,根据正弦定理得 ,所以
,所以 ,
,
由 为锐角三角形得
为锐角三角形得 .………………………………………………7分
.………………………………………………7分
(Ⅱ)根据余弦定理,得

 .
.
所以, .………………………………………………14分
.………………………………………………14分
17.解:(Ⅰ)记 表示事件:“
表示事件:“ 位顾客中至少
位顾客中至少 位采用一次性付款”,则
位采用一次性付款”,则 表示事件:“
表示事件:“ 位顾客中无人采用一次性付款”.
位顾客中无人采用一次性付款”.
 ,
,
 .………………………………………………7分
.………………………………………………7分
(Ⅱ)记 表示事件:“
表示事件:“ 位顾客每人购买
位顾客每人购买 件该商品,商场获得利润不超过
件该商品,商场获得利润不超过 元”.
元”.
 表示事件:“购买该商品的
表示事件:“购买该商品的 位顾客中无人采用分期付款”.
位顾客中无人采用分期付款”.
 表示事件:“购买该商品的
表示事件:“购买该商品的 位顾客中恰有
位顾客中恰有 位采用分期付款”.
位采用分期付款”.
则 .
.
 ,
, .
.



 .……………………………………14分
.……………………………………14分
18.解法一:(1)作 ,垂足为
,垂足为 ,连结
,连结 ,由侧面
,由侧面 底面
底面 ,得
,得 底面
底面 .
.
 因为
因为 ,所以
,所以 ,又
,又 ,故
,故 为等腰直角三角形,
为等腰直角三角形, ,
,
由三垂线定理,得 .………………………7分
.………………………7分
(Ⅱ)由(Ⅰ)知 ,
,
依题设 ,
,
故 ,由
,由 ,
, ,
, .
.
又 ,作
,作 ,垂足为
,垂足为 ,
,
则 平面
平面 ,连结
,连结 .
. 为直线
为直线 与平面
与平面 所成的角.
所成的角.

所以,直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 .………………………………………………14分
.………………………………………………14分
解法二:(Ⅰ)作 ,垂足为
,垂足为 ,连结
,连结 ,由侧面
,由侧面 底面
底面 ,得
,得 平面
平面 .
.
因为 ,所以
,所以 .
.
 又
又 ,
, 为等腰直角三角形,
为等腰直角三角形, .
.
如图,以 为坐标原点,
为坐标原点, 为
为 轴正向,建立直角坐标系
轴正向,建立直角坐标系 ,
,
因为 ,
, ,
,
又 ,所以
,所以 ,
,
 ,
, .
.
 ,
, ,
, ,
, ,所以
,所以 .…………………7分
.…………………7分
(Ⅱ) ,
, .
.
 与
与 的夹角记为
的夹角记为 ,
, 与平面
与平面 所成的角记为
所成的角记为 ,因为
,因为 为平面
为平面 的法向量,所以
的法向量,所以 与
与 互余.
互余.
 ,
, ,
,
所以,直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 .………………………14分
.………………………14分
19.解:(Ⅰ) ,
,
因为函数 在
在 及
及 取得极值,则有
取得极值,则有 ,
, .
.
即
解得 ,
, .………………………7分
.………………………7分
(Ⅱ)由(Ⅰ)可知, ,
,
 .
.
当 时,
时, ;
;
当 时,
时, ;
;
当 时,
时, .
.
所以,当 时,
时, 取得极大值
取得极大值 ,又
,又 ,
, .
.
则当 时,
时, 的最大值为
的最大值为 .
.
因为对于任意的 ,有
,有 恒成立,
恒成立,
所以  ,
,
解得  或
或 ,
,
因此 的取值范围为
的取值范围为 .………………………14分
.………………………14分
20.解:(Ⅰ)设 的公差为
的公差为 ,
, 的公比为
的公比为 ,则依题意有
,则依题意有 且
且
解得 ,
, .
.
所以 ,
,
 .………………………6分
.………………………6分
(Ⅱ) .
.
 ,①
,①
 ,②
,②
②-①得 ,
,


 .………………………12分
.………………………12分
 21.证明:(Ⅰ)椭圆的半焦距
21.证明:(Ⅰ)椭圆的半焦距 ,
,
由 知点
知点 在以线段
在以线段 为直径的圆上,
为直径的圆上,
故 ,
,
所以, .………………………6分
.………………………6分
(Ⅱ)(?)当 的斜率
的斜率 存在且
存在且 时,
时, 的方程为
的方程为 ,代入椭圆方程
,代入椭圆方程 ,并化简得
,并化简得 .
.
设 ,
, ,则
,则
 ,
, ,
,
 ;
;
因为 与
与 相交于点
相交于点 ,且
,且 的斜率为
的斜率为 .
.
所以, .
.
四边形 的面积
的面积
 .
.
当 时,上式取等号.………………………10分
时,上式取等号.………………………10分
(?)当 的斜率
的斜率 或斜率不存在时,四边形
或斜率不存在时,四边形 的面积
的面积 .……………………11分
.……………………11分
综上,四边形 的面积的最小值为
的面积的最小值为 .………………………12分
.………………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com