
题目列表(包括答案和解析)
、(本题15分)已知函数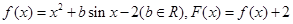 ,且对于任意实数
,且对于任意实数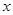 ,恒有F(x)=F(-x)。(1)求函数
,恒有F(x)=F(-x)。(1)求函数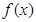 的解析式;
的解析式;
(2)已知函数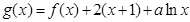 在区间
在区间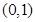 上单调,求实数
上单调,求实数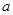 的取值范围;
的取值范围;
(3)函数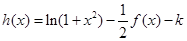 有几个零点?
有几个零点?
、有如图(表1)所示的3行5列的数表,其中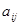 表示第
表示第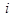 行第
行第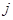 列的数字,这15个数字中恰有1,2,3,4,5各3个。按预定规则取出这些数字中的部分或全部,形成一个数列
列的数字,这15个数字中恰有1,2,3,4,5各3个。按预定规则取出这些数字中的部分或全部,形成一个数列 。规则如下:(1)先取出
。规则如下:(1)先取出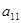 ,并记
,并记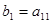 ;若
;若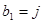 ,则从第
,则从第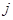 列取出行号最小的数字,并记作
列取出行号最小的数字,并记作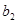 ;(2)以此类推,当
;(2)以此类推,当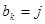 时,就从第
时,就从第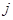 列取出现存行号最小的那个数记作
列取出现存行号最小的那个数记作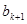 ;直到无法进行就终止。例如由(表(2)可以得到数列
;直到无法进行就终止。例如由(表(2)可以得到数列 :1,2,4,5,3,2,5,1,3,1. 试问数列
:1,2,4,5,3,2,5,1,3,1. 试问数列 的项数恰为15的概率为
。
的项数恰为15的概率为
。
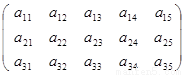
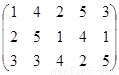
(表1) ( 表2)
(15分)某地位于甲、乙两条河流的交汇处,根据统计资料预测,今年汛期甲河流发生洪水的概率为0.25,乙河流发生洪水的概率为0.18(假设两河流发生洪水与否互不影响).现有一台大型设备正在该地工作,为了保护设备,施工部门提出以下三种方案:
方案1:运走设备,此时需花费4000元;
方案2:建一保护围墙,需花费1000元,但围墙只能抵御一个河流发生的洪水,当两河流同时发生洪水时,设备仍将受损,损失约56 000元;
方案3:不采取措施,此时,当两河流都发生洪水时损失达60000元,只有一条河流发生洪水时,损失为10000元.
(1)试求方案3中损失费X(随机变量)的分布列;
(2)试比较哪一种方案好.
、有如图(表1)所示的3行5列的数表,其中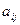 表示第
表示第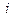 行第
行第 列的数字,这15个数字中恰有1,2,3,4,5各3个。按预定规则取出这些数字中的部分或全部,形成一个数列
列的数字,这15个数字中恰有1,2,3,4,5各3个。按预定规则取出这些数字中的部分或全部,形成一个数列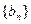 。规则如下:(1)先取出
。规则如下:(1)先取出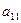 ,并记
,并记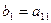 ;若
;若 ,则从第
,则从第 列取出行号最小的数字,并记作
列取出行号最小的数字,并记作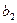 ;(2)以此类推,当
;(2)以此类推,当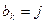 时,就从第
时,就从第 列取出现存行号最小的那个数记作
列取出现存行号最小的那个数记作 ;直到无法进行就终止。例如由(表(2)可以得到数列
;直到无法进行就终止。例如由(表(2)可以得到数列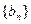 :1,2,4
:1,2,4 ,5,3,2,5,1,3,1. 试问数列
,5,3,2,5,1,3,1. 试问数列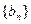 的项数恰为15的概率为 。
的项数恰为15的概率为 。
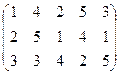
(表1) ( 表2)
 表示第
表示第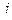 行第
行第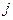 列的数字,这15个数字中恰有1,2,3,4,5各3个。按预定规则取出这些数字中的部分或全部,形成一个数列
列的数字,这15个数字中恰有1,2,3,4,5各3个。按预定规则取出这些数字中的部分或全部,形成一个数列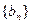 。规则如下:(1)先取出
。规则如下:(1)先取出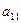 ,并记
,并记 ;若
;若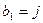 ,则从第
,则从第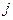 列取出行号最小的数字,并记作
列取出行号最小的数字,并记作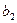 ;(2)以此类推,当
;(2)以此类推,当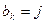 时,就从第
时,就从第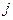 列取出现存行号最小的那个数记作
列取出现存行号最小的那个数记作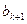 ;直到无法进行就终止。例如由(表(2)可以得到数列
;直到无法进行就终止。例如由(表(2)可以得到数列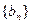 :1,2,4
:1,2,4 ,5,3,2,5,1,3,1. 试问数列
,5,3,2,5,1,3,1. 试问数列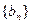 的项数恰为15的概率为 。
的项数恰为15的概率为 。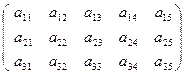
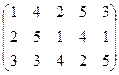
一. DCADB CCDAC
二.11.
(测试试题卷(07-11-17).files/image193.gif) ,3)∪(3,4)12.
,3)∪(3,4)12. 测试试题卷(07-11-17).files/image195.gif) 13. 2 14. 9
15. 1
13. 2 14. 9
15. 1
16.解:(Ⅰ)由已知得:测试试题卷(07-11-17).files/image197.gif) ,
……………………… (3分)
,
……………………… (3分)
又测试试题卷(07-11-17).files/image199.gif) 是△ABC的内角,所以
是△ABC的内角,所以测试试题卷(07-11-17).files/image201.gif) . ………………………………… (6分)
. ………………………………… (6分)
(2)由正弦定理:测试试题卷(07-11-17).files/image203.gif) ,
,测试试题卷(07-11-17).files/image205.gif) ………………9分
………………9分
又因为测试试题卷(07-11-17).files/image207.gif) ,
,测试试题卷(07-11-17).files/image209.gif) ,又
,又测试试题卷(07-11-17).files/image211.gif) 是△ABC的内角,所以
是△ABC的内角,所以测试试题卷(07-11-17).files/image213.gif) .………………12分
.………………12分
17.解:(I)由测试试题卷(07-11-17).files/image215.gif) ,得
,得测试试题卷(07-11-17).files/image217.gif) .??????????????4分
.??????????????4分
(II)测试试题卷(07-11-17).files/image219.gif) .????????????????7分
.????????????????7分
由测试试题卷(07-11-17).files/image221.gif) ,得
,得测试试题卷(07-11-17).files/image223.gif) ,又
,又测试试题卷(07-11-17).files/image152.gif) ,所以
,所以测试试题卷(07-11-17).files/image226.gif) ,??????????11分
,??????????11分
即测试试题卷(07-11-17).files/image154.gif) 的取值范围是
的取值范围是测试试题卷(07-11-17).files/image229.gif) .????????????????????????12分
.????????????????????????12分
18. 解:
(1) 测试试题卷(07-11-17).files/image231.gif) .…………………………6分
.…………………………6分
(2)原式测试试题卷(07-11-17).files/image233.gif)
测试试题卷(07-11-17).files/image235.gif) .……………………………………………8分
.……………………………………………8分
19、解:(1)
测试试题卷(07-11-17).files/image237.gif) … 2分
… 2分
则测试试题卷(07-11-17).files/image070.gif) 的最小正周期
的最小正周期测试试题卷(07-11-17).files/image239.gif) , ???????????????????4分
, ???????????????????4分
且当测试试题卷(07-11-17).files/image241.gif) 时
时测试试题卷(07-11-17).files/image070.gif) 单调递增.
单调递增.
即测试试题卷(07-11-17).files/image243.gif) 为
为测试试题卷(07-11-17).files/image070.gif) 的单调递增区间(写成开区间不扣分).??7分
的单调递增区间(写成开区间不扣分).??7分
(2)当测试试题卷(07-11-17).files/image165.gif) 时
时测试试题卷(07-11-17).files/image245.gif) ,当
,当测试试题卷(07-11-17).files/image247.gif) ,即
,即测试试题卷(07-11-17).files/image249.gif) 时
时测试试题卷(07-11-17).files/image251.gif) .
.
所以测试试题卷(07-11-17).files/image253.gif) .?????????????????11分
.?????????????????11分
测试试题卷(07-11-17).files/image255.gif) 为
为测试试题卷(07-11-17).files/image070.gif) 的对称轴.??????????14分
的对称轴.??????????14分
20.解:(Ⅰ)∵测试试题卷(07-11-17).files/image257.gif) ,当
,当测试试题卷(07-11-17).files/image259.gif) 时,
时,测试试题卷(07-11-17).files/image261.gif) .
.
∴测试试题卷(07-11-17).files/image070.gif) 在[1,3]上是增函数.---------------------------------3分
在[1,3]上是增函数.---------------------------------3分
∴当测试试题卷(07-11-17).files/image259.gif) 时,
时,测试试题卷(07-11-17).files/image264.gif) ≤
≤测试试题卷(07-11-17).files/image070.gif) ≤
≤测试试题卷(07-11-17).files/image266.gif) ,即 -2≤
,即 -2≤测试试题卷(07-11-17).files/image070.gif) ≤26.
≤26.
所以当测试试题卷(07-11-17).files/image268.gif) 时,
时,测试试题卷(07-11-17).files/image270.gif) 当
当测试试题卷(07-11-17).files/image272.gif) 时,
时,测试试题卷(07-11-17).files/image274.gif) ----4分
----4分
∴存在常数M=26,使得测试试题卷(07-11-17).files/image276.gif) ,都有
,都有测试试题卷(07-11-17).files/image178.gif) ≤M成立.
≤M成立.
故函数测试试题卷(07-11-17).files/image180.gif) 是[1,3]上的有界函数.---------------------------6分
是[1,3]上的有界函数.---------------------------6分
(Ⅱ)∵测试试题卷(07-11-17).files/image280.gif) . 由
. 由测试试题卷(07-11-17).files/image282.gif) ≤1,得
≤1,得测试试题卷(07-11-17).files/image284.gif) ≤1----------------8分
≤1----------------8分
∴测试试题卷(07-11-17).files/image286.gif)
测试试题卷(07-11-17).files/image288.gif) ------------------------10分
------------------------10分
令测试试题卷(07-11-17).files/image290.gif) ,显然
,显然测试试题卷(07-11-17).files/image292.gif) 在
在测试试题卷(07-11-17).files/image294.gif) 上单调递减,
上单调递减,
则当t→+∞时,测试试题卷(07-11-17).files/image292.gif) →1. ∴
→1. ∴测试试题卷(07-11-17).files/image297.gif)
令测试试题卷(07-11-17).files/image299.gif) ,显然
,显然测试试题卷(07-11-17).files/image301.gif) 在
在测试试题卷(07-11-17).files/image294.gif) 上单调递减,
上单调递减,
则当测试试题卷(07-11-17).files/image303.gif) 时,
时,测试试题卷(07-11-17).files/image305.gif) ∴
∴测试试题卷(07-11-17).files/image307.gif)
∴0≤a≤1;
故所求a的取值范围为0≤a≤1. -------------14分
21.解:(I) 由题意得 f (e) = pe--2ln e = qe- -2 ………… 1分
Þ (p-q) (e + ) = 0 ………… 2分
而 e + ≠0
∴ p = q ………… 3分
(II) 由 (I) 知 f (x) = px--2ln x
f’(x) = p + -= ………… 4分
令 h(x) = px 2-2x + p,要使 f (x) 在其定义域 (0,+¥) 内为单调函数,只需 h(x) 在 (0,+¥) 内满足:h(x)≥0 或 h(x)≤0 恒成立. ………… 5分
① 当 p = 0时, h(x) = -2x,∵ x > 0,∴ h(x) < 0,∴ f’(x) = - < 0,
∴ f (x) 在 (0,+¥) 内为单调递减,故 p = 0适合题意. ………… 6分
② 当 p > 0时,h(x) = px 2-2x + p,其图象为开口向上的抛物线,对称轴为 x = ∈(0,+¥),∴ h(x)min = p-
只需 p-≥1,即 p≥1 时 h(x)≥0,f’(x)≥0
∴ f (x) 在 (0,+¥) 内为单调递增,
故 p≥1适合题意. ………… 7分
③ 当 p < 0时,h(x) = px 2-2x + p,其图象为开口向下的抛物线,对称轴为 x = Ï (0,+¥)
只需 h(0)≤0,即 p≤0时 h(x)≤0在 (0,+¥) 恒成立.
故 p < 0适合题意. ………… 8分
综上可得,p≥1或 p≤0 ………… 9分
另解:(II) 由 (I) 知 f (x) = px--2ln x
f’(x) = p + -= p (1 + )- ………… 4分
要使 f (x) 在其定义域 (0,+¥) 内为单调函数,只需 f’(x) 在 (0,+¥) 内满足:f’(x)≥0 或 f’(x)≤0 恒成立. ………… 5分
由 f’(x)≥0 Û p (1 + )-≥0 Û p≥ Û p≥()max,x > 0
∵ ≤ = 1,且 x = 1 时等号成立,故 ()max = 1
∴ p≥1 ………… 7分
由 f’(x)≤0 Û p (1 + )-≤0 Û p≤ Û p≤()min,x > 0
而 > 0 且 x → 0 时,→ 0,故 p≤0 ………… 8分
综上可得,p≥1或 p≤0 ………… 9分
(III) ∵ g(x) = 在 [1,e] 上是减函数
∴ x = e 时,g(x)min = 2,x = 1 时,g(x)max = 2e
即 g(x) Î [2,2e] ………… 10分
① p≤0 时,由 (II) 知 f (x) 在 [1,e] 递减 Þ f (x)max = f (1) = 0 < 2,不合题意。 …11分
② 0 < p < 1 时,由x Î [1,e] Þ x-≥0
∴ f (x) = p (x-)-2ln x≤x--2ln x
右边为 f (x) 当 p = 1 时的表达式,故在 [1,e] 递增
∴ f (x)≤x--2ln x≤e--2ln e = e--2 < 2,不合题意。 ………… 12分
③ p≥1 时,由 (II) 知 f (x) 在 [1,e] 连续递增,f (1) = 0 < 2,又g(x) 在 [1,e] 上是减函数
∴ 本命题 Û f (x)max > g(x)min = 2,x Î [1,e]
Þ f (x)max = f (e) = p (e-)-2ln e > 2
Þ p > ………… 13分
综上,p 的取值范围是 (,+¥) ………… 14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com