
题目列表(包括答案和解析)
有下列命题:
①在空间中,若![]() ;
;
②直角梯形是平面图形;
③{正四棱柱}![]() {长方体};
{长方体};
④在四面体P-ABC中,PA⊥BC,PB⊥AC,则点A在平面PBC内的射影恰为△PBC的垂心,其中真命题的个数是
1
2
3
4
有下列命题:①在空间中,若 ,
,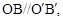 则
则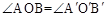 ;②直角梯形是平面图形;③
;②直角梯形是平面图形;③ ; ④若
; ④若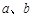 是两条异面直线,
是两条异面直线,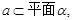
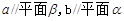 ,则
,则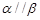 ;⑤在四面体
;⑤在四面体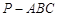 中,
中,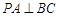 ,
,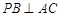 ,则点
,则点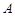 在面
在面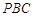 内的射影为
内的射影为 的垂心,其中真命题的个数是( )
的垂心,其中真命题的个数是( )
A.1 B.2 C.3 D.4
有下列命题:①在空间中,若![]() ,
,![]() 则
则![]() ;②直角梯形是平面图形;③
;②直角梯形是平面图形;③![]() ; ④若
; ④若![]() 是两条异面直线,
是两条异面直线,![]()
![]() ,则
,则![]() ;⑤在四面体
;⑤在四面体![]() 中,
中,![]() ,
,![]() ,则点
,则点![]() 在面
在面![]() 内的射影为
内的射影为![]() 的垂心,其中真命题的个数是( )
的垂心,其中真命题的个数是( )
A.1 B.2 C.3 D.4
第I卷(选择题 共60分)
一、选择题(每小题5分,共60分)
1―6ADBADC 7―12ABCBBC
第Ⅱ卷(非选择题 共90分)
二、填空题(每小题4分,共16分)
13.2 14..files/image159.gif) 15.
15..files/image161.gif) 16.①③
16.①③
三、解答题(本大题共6小题,共74分)
17.解:(I).files/image163.gif)
.files/image165.gif)
.files/image167.gif)
.files/image169.gif) 4分
4分
又.files/image171.gif) 2分
2分
(II).files/image173.gif)
.files/image175.gif) 2分
2分
|