20090520
由余弦定理,得 ,所以
,所以 , ……10分
, ……10分
解方程组 ,得
,得 .
……12分
.
……12分
18.解:记 “过第一关”为事件A,“第一关第一次过关”为事件A1,“第一关第二次过关”为事件A2;“过第二关”为事件B, “第二关第一次过关”为事件B1,“第二关第二次过关”为事件B2;
(Ⅰ)该同学获得900元奖金,即该同学顺利通过第一关,但未通过第二关,则所求概率为

 .
……………………………3分
.
……………………………3分
(Ⅱ)该同学通过第一关的概率为:
 , ……………………5分
, ……………………5分
该同学通过第一、二关的概率为:


 , ………………………7分
, ………………………7分
∴ 在该同学已顺利通过第一关的条件下,他获3600元奖金的概率是
 . ………………………………………………………8分
. ………………………………………………………8分
(Ⅲ)该同学获得奖金额 可能取值为:0 元,900 元, 3600 元.………9分
可能取值为:0 元,900 元, 3600 元.………9分
 , ……………………………10分
, ……………………………10分
 ,
,
 ,
,
(另解: =1-
=1- -
- =
= )
)
∴  . ……12分
. ……12分
19.(本题满分12分)
解: (Ⅰ)当 为
为 中点时,有
中点时,有 ∥平面
∥平面 .…1分
.…1分
 证明:连结
证明:连结 连结
连结 ,
,
∵四边形 是矩形 ∴
是矩形 ∴ 为
为 中点
中点
∵ ∥平面
∥平面 ,
,
且 平面
平面 ,
, 平面
平面
∴ ∥
∥ ,------------------4分
,------------------4分
∴ 为
为 的中点.------------------5分
的中点.------------------5分
(Ⅱ)建立空间直角坐标系 如图所示,
如图所示,
则 ,
, ,
, ,
,

 ,
, ------------7分
------------7分
所以
设 为平面
为平面 的法向量,
的法向量,
则有 ,
,
即
令 ,可得平面
,可得平面 的一个
的一个
法向量为 , ----------------9分
, ----------------9分
而平面 的法向量为
的法向量为 , ---------------------------10分
, ---------------------------10分
所以 ,
,
所以二面角 的余弦值为
的余弦值为 ----------------------------12分
----------------------------12分
 20.(Ⅰ)设椭圆C的方程为
20.(Ⅰ)设椭圆C的方程为 ,
,
则由题意知 .
.
∴
∴ .
.
∴椭圆C的方程为  ……………………4分
……………………4分
(Ⅱ)假设右焦点 可以为
可以为 的垂心,
的垂心,
 ,∴直线
,∴直线 的斜率为
的斜率为 ,
,
从而直线 的斜率为1.设其方程为
的斜率为1.设其方程为 , …………………………………5分
, …………………………………5分
联立方程组 ,
,
整理可得: ……………6分.
……………6分.
 ,∴
,∴
设 ,则
,则 ,
,
 .……………7分
.……………7分
于是 

解之得 或
或 .
……………10分
.
……………10分
当 时,点
时,点 即为直线
即为直线 与椭圆的交点,不合题意;
与椭圆的交点,不合题意;
当 时,经检验知
时,经检验知 和椭圆相交,符合题意.
和椭圆相交,符合题意.
所以,当且仅当直线 的方程为
的方程为 时,
时,
点 是
是 的垂心.…………12分
的垂心.…………12分
21.解:(Ⅰ) 的导数
的导数
令 ,解得
,解得 ;令
;令 ,
,
解得 .………………………2分
.………………………2分
从而 在
在 内单调递减,在
内单调递减,在 内单调递增.
内单调递增.
所以,当 时,
时, 取得最小值
取得最小值 .……………………………5分
.……………………………5分
(II)因为不等式 的解集为P,且
的解集为P,且 ,
,
所以,对任意的 ,不等式
,不等式 恒成立,……………………………6分
恒成立,……………………………6分
由 ,得
,得
当 时,上述不等式显然成立,故只需考虑
时,上述不等式显然成立,故只需考虑 的情况。………………7分
的情况。………………7分
将 变形为
变形为 ………………………………………………8分
………………………………………………8分
令 ,则
,则
令 ,解得
,解得 ;令
;令 ,
,
解得 .…………………………10分
.…………………………10分
从而 在
在 内单调递减,在
内单调递减,在 内单调递增.
内单调递增.
所以,当 时,
时,
 取得最小值
取得最小值 ,从而,
,从而,
所求实数 的取值范围是
的取值范围是 .………………12分
.………………12分
22.解:(Ⅰ)当 时,
时,
∴




(Ⅱ)在 中,
中,
在 中,
中, ,
,
当 时,
时, 中第
中第 项是
项是 ,
,
而 中的第
中的第 项是
项是 ,
,
所以 中第
中第 项与
项与 中的第
中的第 项相等.
项相等.
当 时,
时, 中第
中第 项是
项是 ,
,
而 中的第
中的第 项是
项是 ,
,
所以 中第
中第 项与
项与 中的第
中的第 项相等.
项相等.
∴ 
 .
.
(Ⅲ)


 +
+


 .
.
当且仅当 或
或 ,等号成立.
,等号成立.
∴当 或
或 时,
时, 最小.
最小.

 和直线
和直线 ,
, 的直角坐标方程;(2)当
的直角坐标方程;(2)当 时,求直线
时,求直线 与圆O公共点的一个极坐标.
与圆O公共点的一个极坐标.
 和
和 ,不等式
,不等式 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围.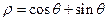 和直线
和直线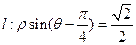 ,
, 的直角坐标方程;(2)当
的直角坐标方程;(2)当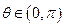 时,求直线
时,求直线 与圆O公共点的一个极坐标.
与圆O公共点的一个极坐标.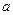
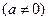 和
和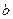 ,不等式
,不等式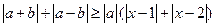 恒成立,试求实数
恒成立,试求实数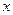 的取值范围.
的取值范围.![]() =
=![]() =
=![]() -ab,所以ab≤
-ab,所以ab≤![]() ,故B错;
,故B错;![]() +
+![]() =
=![]() =
=![]() ≥4,故A错;由基本不等式得
≥4,故A错;由基本不等式得![]() ≤
≤![]() =
=![]() ,即
,即![]() +
+![]() ≤
≤![]() ,故C正确;a2+b2=(a+b)2-2ab=1-2ab≥1-2×
,故C正确;a2+b2=(a+b)2-2ab=1-2ab≥1-2×![]() =
=![]() ,故D错.故选C.
,故D错.故选C. 满足
满足 ,且当
,且当 时,
时, ,则当
,则当 时,
时, 的最小值为( )
的最小值为( ) (B)
(B) (C)
(C) (D)
(D)
 作圆
作圆 的弦,其中弦长为整数的共有 ( )
的弦,其中弦长为整数的共有 ( )  14.6 15.①⑤ 16.
14.6 15.①⑤ 16.
 ,
, , ……3分
, ……3分
 、
、 、
、 是
是 的三内角,所以
的三内角,所以 ,
,  .
……6分
.
……6分