题目列表(包括答案和解析)
某超市在节日期间进行有奖促销，规定凡在该超市购物满400元的顾客，均可获得一次摸奖机会．摸奖规则如下：
奖盒中放有除颜色不同外其余完全相同的4个球（红、黄、黑、白）．顾客不放回的每次摸出1个球，若摸到黑球则摸奖停止，否则就继续摸球．按规定摸到红球奖励20元，摸到白球或黄球奖励10元，摸到黑球不奖励．
（1）求1名顾客摸球2次摸奖停止的概率；
（2）记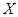
为1名顾客摸奖获得的奖金数额，求随机变量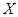的分布列和数学期望．
为1名顾客摸奖获得的奖金数额，求随机变量的分布列和数学期望．（本小题满分13分）
某品牌专卖店准备在春节期间举行促销活动，根据市场调查，该店决定从
种型号的洗衣机，种型号的电视机和
种型号的电脑中，选出种型号的商品进行促销．
（Ⅰ）试求选出的种型号的商品中至少有一种是电脑的概率；
（Ⅱ）该店对选出的商品采用的促销方案是有奖销售，即在该商品现价的基础上将价格提高
元，同时，若顾客购买该商品，则允许有次抽奖的机会，若中奖，则每次中奖都获得
元奖金．假设顾客每次抽奖时获奖与否的概率都是
，设顾客在三次抽奖中所获得的奖金总额（单位：元）为随机变量
，请写出的分布列，并求的数学期望；
（Ⅲ）在（Ⅱ）的条件下，问该店若想采用此促销方案获利，则每次中奖奖金要低于多少元？
某超市在节日期间进行有奖促销，凡在该超市购物满200元的顾客，将获得一次摸奖机会，规则如下：
奖盒中放有除颜色外完全相同的1个红色球，1个黄色球，1个蓝色球和1个黑色球．顾客不放回的每次摸出1个球，直至摸到黑色球停止摸奖．规定摸到红色球奖励10元，摸到黄色球或蓝色球奖励5元，摸到黑色球无奖励．
（1）求一名顾客摸球3次停止摸奖的概率；
（2）记X为一名顾客摸奖获得的奖金数额，求随机变量X的分布列和数学期望．
某超市在节日期间进行有奖促销，凡在该超市购物满400元的顾客，将获得一次摸奖机会，规则如下：奖盒中放有除颜色外完全相同的1个红球，1个黄球，1个白球和1个黑球．顾客不放回的每次摸出1个球，若摸到黑球则停止摸奖，否则就继续摸球．规定摸到红球奖励20元，摸到白球或黄球奖励10元，摸到黑球不奖励．
（1）求1名顾客摸球2次停止摸奖的概率；
（2）记
为1名顾客摸奖获得的奖金数额，求随机变量的分布律和数学期望．
一、选择题
AACCD BBDDD AC
二、填空题
13．
14．6 15．①⑤ 16．
三、解答题
17．解：（Ⅰ）因为
，
由正弦定理，得
， ……3分
整理，得
因为
、
、
是
的三内角，所以
，
因此 
．
……6分
|
，所以
， ……10分
，得
．
……12分
．
……………………………３分
， ……………………5分
， ………………………７分
． ………………………………………………………8分
可能取值为：0 元，900 元， 3600 元．………9分
， ……………………………10分 
， 
，
＝1－
－
＝
）
． ……12分
为
中点时,有
∥平面
．…１分 
证明:连结
连结
，
是矩形 ∴
为
中点
平面
平面
如图所示,
,
,
,
,
------------7分
为平面
,
,可得平面
, ----------------9分
的法向量为
， ---------------------------10分
，
的余弦值为
----------------------------12分
20．（Ⅰ）设椭圆C的方程为
，
．
．
……………………4分
可以为
的垂心，
，∴直线
的斜率为
，
的斜率为1．设其方程为
， …………………………………５分
，
……………6分．
，∴
，则
，
．……………7分
或
．
……………10分
时, 
的导数
，解得
；令
，
．………………………2分
内单调递减，在
内单调递增．
时，
．……………………………5分
的解集为P，且
，
，不等式
的情况。………………7分
………………………………………………8分
，则
，解得
；令
，
．…………………………10分
在
内单调递减，在
内单调递增．
时，
，从而，
的取值范围是
．………………12分
时，
中，
中，
，
时，
项是
，
项是
，
时，
，
项是
，
．
+
．
或
，等号成立．