
题目列表(包括答案和解析)
| 2 | 3 |
| 2 |
| 2 |
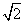 时,数列{bn}中的任意三项都不能构成等比数列;
时,数列{bn}中的任意三项都不能构成等比数列;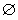 ,若存在,求出b的一切可能的取值及相应的集合C;若不存在,说明理由。
,若存在,求出b的一切可能的取值及相应的集合C;若不存在,说明理由。 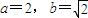 时,数列{bn}中的任意三项都不能构成等比数列;
时,数列{bn}中的任意三项都不能构成等比数列;
一、填空题
1.-----理科数学.files/image208.gif) 2.
2. -----理科数学.files/image210.gif) 3.2 4.
3.2 4.-----理科数学.files/image212.gif) 5. i
5. i-----理科数学.files/image214.gif) 100 6.
100 6.-----理科数学.files/image216.gif) 7. 2
7. 2
8. -----理科数学.files/image218.gif) 9.
9. -----理科数学.files/image220.gif) 10.
10. -----理科数学.files/image222.gif) 11.
11. -----理科数学.files/image224.gif) 12.
12.-----理科数学.files/image226.gif)
二、选择题
13. -----理科数学.files/image228.gif) 14.A 15.A. 16. D
14.A 15.A. 16. D
三、解答题
17.
(1)由题意可得:-----理科数学.files/image106.gif) =5----------------------------------------------------------(2分)
=5----------------------------------------------------------(2分)
由:-----理科数学.files/image230.gif) 得:
得:-----理科数学.files/image111.gif) =314---------------------------------------(4分)
=314---------------------------------------(4分)
或:-----理科数学.files/image232.gif) ,
,-----理科数学.files/image234.gif)
(2)方法一:由:-----理科数学.files/image236.gif) 或
或-----理科数学.files/image238.gif) ------(1分)
------(1分)
-----理科数学.files/image240.gif) 或
或-----理科数学.files/image242.gif) ---------(1分)
---------(1分)
得:-----理科数学.files/image244.gif) 0.0110-----------------------------------------------------------------(1分)
0.0110-----------------------------------------------------------------(1分)
方法二:由:-----理科数学.files/image246.gif)
得:-----理科数学.files/image248.gif) -----------------------------------------------------------------(1分)
-----------------------------------------------------------------(1分)
由:-----理科数学.files/image113.gif) 点和
点和-----理科数学.files/image115.gif) 点的纵坐标相等,可得
点的纵坐标相等,可得-----理科数学.files/image113.gif) 点和
点和-----理科数学.files/image115.gif) 点关于
点关于-----理科数学.files/image133.gif) 点对称
点对称
即:-----理科数学.files/image253.gif) ------------------------------------------------------------(1分)
------------------------------------------------------------(1分)
得:-----理科数学.files/image244.gif) 0.011-----------------------------------------------------------------------(1分)
0.011-----------------------------------------------------------------------(1分)
18.(1)-----理科数学.files/image255.gif) ,
,-----理科数学.files/image257.gif) 是等腰三角形,
是等腰三角形,
-----理科数学.files/image259.jpg) 又
又-----理科数学.files/image133.gif) 是
是-----理科数学.files/image135.gif) 的中点,
的中点,-----理科数学.files/image263.gif) ,--------------(1分)
,--------------(1分)
又-----理科数学.files/image265.gif) 底面
底面-----理科数学.files/image267.gif) .
.-----理科数学.files/image269.gif) .----(2分)
.----(2分)
-----理科数学.files/image271.gif) -------------------------------(1分)
-------------------------------(1分)
于是-----理科数学.files/image273.gif) 平面
平面-----理科数学.files/image143.gif) .----------------------(1分)
.----------------------(1分)
(2)过-----理科数学.files/image228.gif) 作
作-----理科数学.files/image277.gif) ,连接
,连接-----理科数学.files/image279.gif) ----------------(1分)
----------------(1分)
-----理科数学.files/image281.gif) 平面
平面-----理科数学.files/image143.gif) ,
,
-----理科数学.files/image284.gif) ,-----------------------------------(1分)
,-----------------------------------(1分)
-----理科数学.files/image286.gif) 平面
平面-----理科数学.files/image147.gif) ,---------------------------(1分)
,---------------------------(1分)
-----理科数学.files/image289.gif) 就是直线
就是直线-----理科数学.files/image145.gif) 与平面
与平面-----理科数学.files/image147.gif) 所成角。---(2分)
所成角。---(2分)
在-----理科数学.files/image291.gif) 中,
中,-----理科数学.files/image293.gif)
-----理科数学.files/image295.gif) ----------------------------------(2分)
----------------------------------(2分)
所以,直线-----理科数学.files/image145.gif) 与平面
与平面-----理科数学.files/image147.gif) 所成角
所成角-----理科数学.files/image297.gif) --------(1分)
--------(1分)
19.解:
(1)函数-----理科数学.files/image158.gif) 的定义域为
的定义域为-----理科数学.files/image299.gif) ;------------------------------------(1分)
;------------------------------------(1分)
当-----理科数学.files/image301.gif) 时
时-----理科数学.files/image303.gif) ;当
;当-----理科数学.files/image305.gif) 时
时-----理科数学.files/image303.gif) ;--------------------------------------------------(1分)
;--------------------------------------------------(1分)
所以,函数-----理科数学.files/image158.gif) 在定义域
在定义域-----理科数学.files/image299.gif) 上不是单调函数,------------------(1分)
上不是单调函数,------------------(1分)
所以它不是“-----理科数学.files/image106.gif) 类函数” ------------------------------------------------------------------(1分)
类函数” ------------------------------------------------------------------(1分)
(2)当-----理科数学.files/image162.gif) 小于0时,则函数
小于0时,则函数-----理科数学.files/image160.gif) 不构成单调函数;(1分)
不构成单调函数;(1分)
当-----理科数学.files/image162.gif) =0时,则函数
=0时,则函数-----理科数学.files/image308.gif) 单调递增,
单调递增,
但在-----理科数学.files/image299.gif) 上不存在定义域是
上不存在定义域是-----理科数学.files/image152.gif) 值域也是
值域也是-----理科数学.files/image152.gif) 的区间
的区间-----理科数学.files/image152.gif) ---------------(1分)
---------------(1分)
当-----理科数学.files/image162.gif) 大于0时,函数
大于0时,函数-----理科数学.files/image160.gif) 在定义域里单调递增,----(1分)
在定义域里单调递增,----(1分)
要使函数-----理科数学.files/image160.gif) 是“
是“-----理科数学.files/image106.gif) 类函数”,
类函数”,
即存在两个不相等的常数-----理科数学.files/image310.gif) ,
,-----理科数学.files/image312.gif)
使得-----理科数学.files/image314.gif) 同时
同时-----理科数学.files/image316.gif) 成立,------------------------------------(1分)
成立,------------------------------------(1分)
即关于-----理科数学.files/image077.gif) 的方程
的方程-----理科数学.files/image319.gif) 有两个不相等的实根,--------------------------------(2分)
有两个不相等的实根,--------------------------------(2分)
-----理科数学.files/image321.gif) ,--------------------------------------------------------------------------(1分)
,--------------------------------------------------------------------------(1分)
亦即直线-----理科数学.files/image323.gif) 与曲线
与曲线-----理科数学.files/image325.gif) 在
在-----理科数学.files/image299.gif) 上有两个不同的交点,-(1分)
上有两个不同的交点,-(1分)
所以,-----理科数学.files/image327.gif) -------------------------------------------------------------------------------(2分)
-------------------------------------------------------------------------------(2分)
20.解:
(1)-----理科数学.files/image329.gif)
-----理科数学.files/image331.gif)
若-----理科数学.files/image333.gif) ,由
,由-----理科数学.files/image335.gif) ,得数列
,得数列-----理科数学.files/image173.gif) 构成等比数列------------------(3分)
构成等比数列------------------(3分)
若-----理科数学.files/image337.gif) ,
,-----理科数学.files/image339.gif) ,数列
,数列-----理科数学.files/image173.gif) 不构成等比数列--------------------------------------(1分)
不构成等比数列--------------------------------------(1分)
(2)由-----理科数学.files/image341.gif) ,得:
,得:-----理科数学.files/image343.gif) -------------------------------------(1分)
-------------------------------------(1分)
-----理科数学.files/image345.gif) ---------------------------------------------------------(1分)
---------------------------------------------------------(1分)
-----理科数学.files/image347.gif) ----------------------------------------------(1分)
----------------------------------------------(1分)
-----理科数学.files/image349.gif)
-----理科数学.files/image351.gif)
-----理科数学.files/image353.gif) ----(1分)
----(1分)
-----理科数学.files/image355.gif) ------------------------------------------------------------------(1分)
------------------------------------------------------------------(1分)
-----理科数学.files/image357.gif) ---------------------------------------------------------------------(1分)
---------------------------------------------------------------------(1分)
(3)若对任意-----理科数学.files/image187.gif) ,不等式
,不等式-----理科数学.files/image189.gif) 恒成立,
恒成立,
即:-----理科数学.files/image359.gif)
-----理科数学.files/image361.gif) -------------------------------------------(1分)
-------------------------------------------(1分)
令:-----理科数学.files/image363.gif) ,当
,当-----理科数学.files/image365.gif) 时,
时,-----理科数学.files/image367.gif) 有最大值为0---------------(1分)
有最大值为0---------------(1分)
令:-----理科数学.files/image369.gif)
-----理科数学.files/image371.gif) ------------------------------------------------------(1分)
------------------------------------------------------(1分)
当-----理科数学.files/image373.gif) 时
时
-----理科数学.files/image375.gif)
-----理科数学.files/image377.gif) ---------------------------------------------------------(1分)
---------------------------------------------------------(1分)
所以,数列-----理科数学.files/image379.gif) 从第二项起单调递减
从第二项起单调递减
当-----理科数学.files/image381.gif) 时,
时,-----理科数学.files/image383.gif) 取得最大值为1-------------------------------(1分)
取得最大值为1-------------------------------(1分)
所以,当-----理科数学.files/image385.gif) 时,不等式
时,不等式-----理科数学.files/image189.gif) 恒成立---------(1分)
恒成立---------(1分)
21. 解:
(1)双曲线-----理科数学.files/image191.gif) 焦点坐标为
焦点坐标为-----理科数学.files/image387.gif) ,渐近线方程
,渐近线方程-----理科数学.files/image389.gif) ---(2分)
---(2分)
双曲线-----理科数学.files/image195.gif) 焦点坐标
焦点坐标-----理科数学.files/image387.gif) ,渐近线方程
,渐近线方程-----理科数学.files/image392.gif) ----(2分)
----(2分)
(2)-----理科数学.files/image393.jpg)
得方程:-----理科数学.files/image395.gif) -------------------------------------------(1分)
-------------------------------------------(1分)
设直线分别与双曲线-----理科数学.files/image191.gif) 的交点
的交点-----理科数学.files/image397.gif) 、
、-----理科数学.files/image228.gif) 的坐标分别为
的坐标分别为-----理科数学.files/image400.gif)
-----理科数学.files/image402.gif) ,线段
,线段-----理科数学.files/image397.gif)
-----理科数学.files/image228.gif) 中点为
中点为-----理科数学.files/image113.gif) 坐标为
坐标为-----理科数学.files/image405.gif)
-----理科数学.files/image407.gif) ----------------------------------------------------------(1分)
----------------------------------------------------------(1分)
-----理科数学.files/image408.jpg)
得方程:-----理科数学.files/image410.gif) ----------------------------------------(1分)
----------------------------------------(1分)
设直线分别与双曲线-----理科数学.files/image195.gif) 的交点
的交点-----理科数学.files/image106.gif) 、
、-----理科数学.files/image133.gif) 的坐标分别为
的坐标分别为-----理科数学.files/image415.gif)
-----理科数学.files/image417.gif) ,线段
,线段-----理科数学.files/image106.gif)
-----理科数学.files/image133.gif) 中点为
中点为-----理科数学.files/image115.gif) 坐标为
坐标为-----理科数学.files/image420.gif)
-----理科数学.files/image422.gif) ---------------------------------------------------(1分)
---------------------------------------------------(1分)
由-----理科数学.files/image424.gif) ,-----------------------------------------------------------(1分)
,-----------------------------------------------------------(1分)
所以,线段-----理科数学.files/image201.gif) 与
与-----理科数学.files/image203.gif) 不相等------------------------------------(1分)
不相等------------------------------------(1分)
(3)
若直线-----理科数学.files/image011.gif) 斜率不存在,交点总个数为4;-------------------------(1分)
斜率不存在,交点总个数为4;-------------------------(1分)
若直线-----理科数学.files/image011.gif) 斜率存在,设斜率为
斜率存在,设斜率为-----理科数学.files/image162.gif) ,直线
,直线-----理科数学.files/image011.gif) 方程为
方程为-----理科数学.files/image427.gif)
直线-----理科数学.files/image011.gif) 与双曲线
与双曲线-----理科数学.files/image191.gif) :
:
-----理科数学.files/image428.jpg)
得方程:-----理科数学.files/image430.gif) ①
①
直线-----理科数学.files/image011.gif) 与双曲线
与双曲线-----理科数学.files/image195.gif) :
:
-----理科数学.files/image431.jpg)
得方程: -----理科数学.files/image433.gif) ②-----------(1分)
②-----------(1分)
-----理科数学.files/image162.gif) 的取值
的取值
直线-----理科数学.files/image011.gif) 与双曲线
与双曲线-----理科数学.files/image191.gif) 右支的交点个数
右支的交点个数
直线-----理科数学.files/image011.gif) 与双曲线
与双曲线-----理科数学.files/image195.gif) 右支的交点个数
右支的交点个数
交点总个数
-----理科数学.files/image435.gif)
1个(交点-----理科数学.files/image437.gif) )
)
1个(交点-----理科数学.files/image439.gif) )
)
2个
-----理科数学.files/image441.gif)
1个(-----理科数学.files/image443.gif) ,
,-----理科数学.files/image445.gif) )
)
1个(-----理科数学.files/image443.gif) ,
,-----理科数学.files/image447.gif) )
)
2个
-----理科数学.files/image449.gif)
1个(与渐进线平行)
1个(理由同上)
2个
-----理科数学.files/image451.gif)
2个(-----理科数学.files/image443.gif) ,方程①两根都大于2)
,方程①两根都大于2)
1个(理由同上)
3个
-----理科数学.files/image453.gif)
2个(理由同上)
1个(与渐进线平行)
3个
-----理科数学.files/image455.gif)
2个(理由同上)
2个(-----理科数学.files/image443.gif) ,方程②
,方程②
两根都大于1)
4个
得:-------------------------------------------------------------------(3分)
由双曲线的对称性可得:
-----理科数学.files/image162.gif) 的取值
的取值
交点总个数
-----理科数学.files/image457.gif)
2个
-----理科数学.files/image459.gif)
2个
-----理科数学.files/image461.gif)
3个
-----理科数学.files/image463.gif)
3个
-----理科数学.files/image465.gif)
4个
得:-------------------------------------------------------------------(2分)
综上所述:(1)若直线-----理科数学.files/image011.gif) 斜率不存在,交点总个数为4;
斜率不存在,交点总个数为4;
(2)若直线-----理科数学.files/image011.gif) 斜率存在,当
斜率存在,当-----理科数学.files/image467.gif) 时,交点总个数为2个;当
时,交点总个数为2个;当-----理科数学.files/image469.gif) 或
或-----理科数学.files/image471.gif) 时,交点总个数为3个;当
时,交点总个数为3个;当-----理科数学.files/image455.gif) 或
或-----理科数学.files/image465.gif) 时,交点总个数为4个;---------------(1分)
时,交点总个数为4个;---------------(1分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com