.files/image196.jpg)
.files/image200.gif) …4分
…4分
(II)由(I)知.files/image202.gif) 平面ABCD
平面ABCD
∴平面PAB⊥平面ABCD. …………4分
在PB上取一点M,作MN⊥AB,则MN⊥平面ABCD,
设MN=h
则.files/image204.gif)
.files/image206.gif) …………6分
…………6分
要使.files/image208.gif)
即M为PB的中点. …………8分
(Ⅲ)连接BD交AC于O,因为AB//CD,AB=2,CD=1,由相似三角形易得BO=2OD
∴O不是BD的中心……………………10分
又∵M为PB的中点
∴在△PBD中,OM与PD不平行
∴OM所以直线与PD所在直线相交
又OM.files/image210.gif) 平面AMC
平面AMC
∴直线PD与平面AMC不平行.……………………12分
20.(本小题满分12分)
解:由图可知M(60,98),N(500,230),C(500,168),MN//CD.
设这两种方案的应付话费与通话时间的函数关系分别为.files/image212.gif) 则
则
.files/image214.gif) ………………2分
………………2分
.files/image216.gif) ……………………4分
……………………4分
(Ⅰ)通话2小时,两种方案的话费分别为116元、168元.………………6分
(Ⅱ)因为.files/image218.gif)
故方案B从500分钟以后,每分钟收费0.3元.………………8分
(每分钟收费即为CD的斜率)
(Ⅲ)由图可知,当.files/image220.gif) ;
;
当.files/image222.gif) ;
;
当.files/image224.gif) ……………………11分
……………………11分
综上,当通话时间在(.files/image226.gif) )时,方案B较方案A优惠.………………12分
)时,方案B较方案A优惠.………………12分
21.(本小题满分12分)
解:(Ⅰ)设.files/image228.gif) 的夹角为
的夹角为.files/image230.gif) ,则
,则.files/image228.gif) 的夹角为
的夹角为.files/image233.gif) ,
,
∵.files/image235.gif)
.files/image237.gif) ……………………2分
……………………2分
又.files/image239.gif)
∴.files/image241.gif) ………………4分
………………4分
(II)设.files/image243.gif) 则
则
.files/image245.gif) …………5分
…………5分
.files/image247.gif)
由.files/image249.gif) …………6分
…………6分
.files/image251.gif) …………7分
…………7分
.files/image253.gif) 上是增函数
上是增函数
.files/image255.gif) 上为增函数
上为增函数
.files/image257.gif) 当m=2时,
当m=2时,.files/image141.gif) 的最小值为
的最小值为.files/image259.gif) …………10分
…………10分
此时P(2,0),椭圆的另一焦点为.files/image261.gif) ,则椭圆长轴长
,则椭圆长轴长
.files/image263.gif)
.files/image265.gif) …………12分
…………12分
22.(本小题满分14分)
解:(I).files/image267.gif) …………2分
…………2分
由.files/image269.gif) …………4分
…………4分
.files/image271.gif)
当.files/image273.gif) 的单调增区间是
的单调增区间是.files/image275.gif) ,单调减区间是
,单调减区间是
.files/image277.gif) …………6分
…………6分
当.files/image279.gif) 的单调增区间是
的单调增区间是.files/image281.gif) ,单调减区间是
,单调减区间是
.files/image283.gif) …………8分
…………8分
(II)当.files/image285.gif) 上单调递增,因此
上单调递增,因此
.files/image287.gif)
…………10分
.files/image289.gif) 上递减,所以值域是
上递减,所以值域是.files/image291.gif)
.files/image293.gif) …………12分
…………12分
因为在.files/image295.gif)
…………13分
.files/image297.gif) 、
、.files/image299.gif) 使得
使得.files/image301.gif) 成立.
成立.
…………14分





![]() ,利用课本中推导等差数列前
,利用课本中推导等差数列前![]() 项和公式的方法,可求得f(-12)+f(-11)+f(-10)+…+f(0)+…+f(12)+f(13)的值是
项和公式的方法,可求得f(-12)+f(-11)+f(-10)+…+f(0)+…+f(12)+f(13)的值是![]()
![]()
![]()
![]()
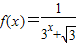 ,利用课本中推导等差数列前n项和公式的方法,可求得f(-12)+f(-11)+f(-10)+…+f(0)+…+f(11)+f(12)+f(13)的值为( )
,利用课本中推导等差数列前n项和公式的方法,可求得f(-12)+f(-11)+f(-10)+…+f(0)+…+f(11)+f(12)+f(13)的值为( )