
2.
求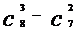 ;
;
1.
计算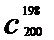 与
与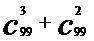 ;
;
(3)定理2还说明了,把从n+1个不同的元素中取出m个元素的组合数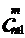 ,等于从n个不同的元素中取出m个元素的组合数
,等于从n个不同的元素中取出m个元素的组合数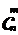 与从n个不同的元素中取出m-1个元素的组合数
与从n个不同的元素中取出m-1个元素的组合数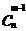 的和。这体现了组合数的可分解性,或组合数的可加性。
的和。这体现了组合数的可分解性,或组合数的可加性。
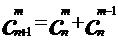 。
。
(3)对于定理2,还可以这样解释:从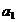 ,
, 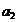 ,….,
,….,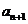 这n+1个不同的元素中取出m个元素的组合数
这n+1个不同的元素中取出m个元素的组合数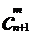 ,这些组合可以分成两类:一类含
,这些组合可以分成两类:一类含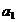 ,一类不含
,一类不含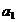 。含
。含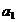 的组合是从
的组合是从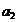 ,….,
,….,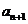 这n个不同的元素中取出m-1个元素的组合数为
这n个不同的元素中取出m-1个元素的组合数为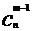 ,不含
,不含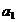 的组合是从
的组合是从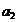 ,….,
,….,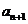 这n个不同的元素中取出m个元素的组合数为
这n个不同的元素中取出m个元素的组合数为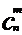 。再由加法原理,得:
。再由加法原理,得:
∴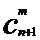
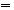
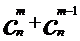
证明:∵ 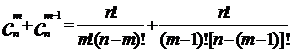
定理2 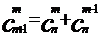 (n,m∈N,且m≤N)
(n,m∈N,且m≤N)
(2) 定理2的证明。要证明这个等式,只要根据组合数的公式变形即可。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com