
(3)是否存在常数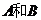 ,同时满足:①当
,同时满足:①当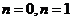 时,有
时,有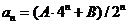 ;② 当
;② 当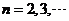 .时,有
.时,有 成立.如果存在满足上述条件的实数
成立.如果存在满足上述条件的实数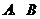 ,求出
,求出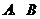 的值;如果不存在,证明你的结论。
的值;如果不存在,证明你的结论。
2007届高三数学第一学期期中测试卷答案
(1)求证: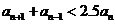 ;(2)设
;(2)设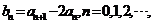 求证:
求证: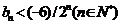 ;
;
21、设函数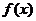 的定义域、值域均为
的定义域、值域均为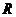 ,
,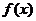 的反函数为
的反函数为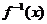 ,且对于任意实数
,且对于任意实数 ,均有
,均有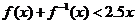 ,定义数列
,定义数列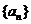 :
: .
.
(1)求点M的轨迹方程;(2)曲线C是由点M轨迹及其关于边AB对称的曲线组成,F(0, 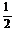 ),过点F的直线交曲线C于P、Q两点,且
),过点F的直线交曲线C于P、Q两点,且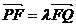 ,求
,求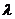 的范围。
的范围。
20、如图边长为2的正方形纸片ABCD,以动直线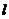 为折痕将正方形向上翻折,使得每次翻折后点B都落在边AD上,记为
为折痕将正方形向上翻折,使得每次翻折后点B都落在边AD上,记为 ;折痕
;折痕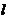 与AB交于点E,点M满足关系式
与AB交于点E,点M满足关系式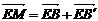 。
。
(3)若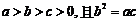 ,求证:
,求证: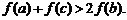
(2)求证: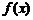 在R上是单调增函数;
在R上是单调增函数;
(1)求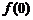 的值,并证明
的值,并证明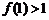 ;
;
①对任意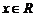 ,有
,有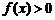 ;②对任意
;②对任意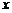 、
、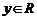 ,有
,有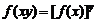 ;③
;③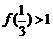
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com