∵－1＜x₁＜x₂＜0，∴x₁－x₂＜0，1－x₁x₂>0.∴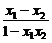＜0，

⑶设－1＜x₁＜x₂＜0，则f(x₁)－f(x₂)＝f(x₁)＋f(－x₂)＝f()，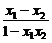

证明:⑴对f(x)＋f(y)＝f(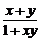)中的x，y，令x＝y＝0，得f(0)＝0，??? 2分

⑵再令y＝－x，又得f(x)＋f(－x)＝f(0)＝0，即f(－x)＝－f(x)，

∴f(x)在x∈(－1，1)上是奇函数. ?????????????????????? 5分

⑷求证:.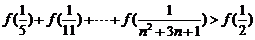

⑶证明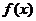在(－1，0)上是单调递减函数；

⑴求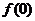的值；

⑵判断函数的奇偶性并给予证明；

20.      (本小题满分14分)定义在(－1，1)上的函数f(x)满足①对任意x、y∈(－1，1)，都有f(x)＋f(y)＝f(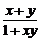);②当x∈(－1，0)时，有f(x)>0。

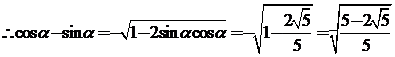。????? 12分

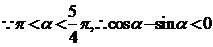???????????????????? 9分

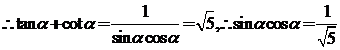??????????? 6分