设方程的两个根为 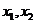，  则根据韦达定理有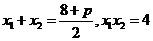

将直线方程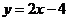代入抛物线方程，并整理得：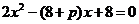

解：设抛物线方程为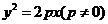

一顶点在坐标原点，焦点在x轴上的抛物线截直线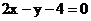所得的弦长为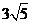，求抛物线的方程。

22．（本题满分14分）

所以动点M的轨迹方程为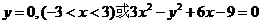

依题意得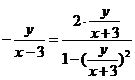：    化简得：

则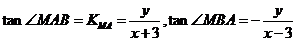

已知两定点A、B距离为6，动点M满足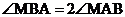，求动点M的轨迹方程。

解：直线AB为x轴，线段AB的垂直平分线为y轴，建立直角坐标系，

  则 A（－3，0），B（3，0），设M（x,y）