
(3)∵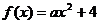 , ∴ F ( x ) =
, ∴ F ( x ) = 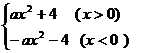 ,
,
∵ mn < 0 , 不妨设 m > 0 , 则 n < 0 , 又 m + n > 0, ∴ m > ? n > 0 , ∴m2 > n2 , ---3分
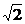 £ x £
£ x £ 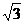 或
或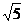 £ x £
£ x £ 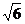 或?
或?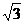 £ x £?
£ x £?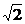 或?
或?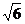 £ x £ ?
£ x £ ?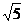 .
---6分
.
---6分
x
> 2时, 解不等式 1 £ 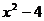 £ 2, 得
£ 2, 得 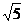 £ x £
£ x £ 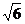 ;
;
综合上述可知原不等式的解为:
0
< x £ 2时,
解不等式 1 £ 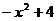 £ 2, 得
£ 2, 得 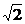 £ x £
£ x £ 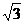 ;
;
F
( x ) = 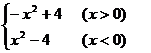 .
--- 2分
.
--- 2分
(2) ∵| F (?x ) | = | F (x ) |, ∴| F (x )|是偶函数, 故可以先求x >0的情况,
当x > 0 时, 由| F (2 )| = 0, 故当
∴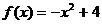 ,
,
19. (本小题满分14分)
(1)∵f (? 2 ) = 0,∴ 4a + 4 = 0, 得 a = ? 1,
∴ tanatanb= ?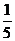 .
--- 4分
.
--- 4分
∴ cos (a+b) =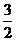 cos (a? b ),
cos (a? b ),
展开得2cosacosb ? 2sinasinb = 3cosacosb + 3sinasinb
即 ? 5sinasinb = cosacosb,
∵ a, b Î A,
=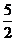 + cos (a+b) ?
+ cos (a+b) ? 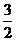 cos (a? b ) =
cos (a? b ) = 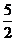 ,
--- 3分
,
--- 3分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com