
20. 解:(Ⅰ)在梯形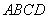 中,由
中,由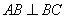 ,
,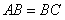 ,得
,得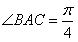 ,∴
,∴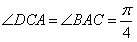 .又
.又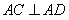 ,故
,故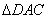 为等腰直角三角形.∴
为等腰直角三角形.∴ .
.
连接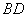 ,交
,交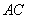 于点
于点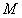 ,则
,则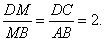

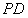 ∥平面
∥平面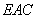 ,又平面
,又平面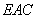
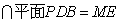 ,∴
,∴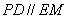
在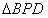 中,
中,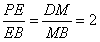 ,
,
即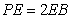 时,
时,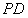 ∥平面
∥平面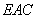
(Ⅱ)方法一:在等腰直角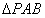 中,取
中,取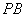 中点
中点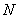 ,连结
,连结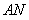 ,则
,则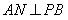 .∵平面
.∵平面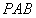 ⊥平面
⊥平面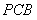 ,且平面
,且平面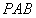
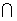 平面
平面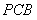 =
=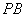 ,∴
,∴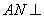 平面
平面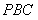 .
.
在平面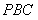 内,过
内,过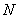 作
作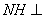 直线
直线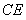 于
于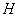 ,连结
,连结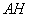 ,由
,由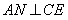 、
、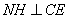 ,得
,得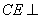 平面
平面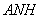 ,故
,故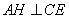 .∴
.∴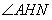 就是二面角
就是二面角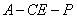 的平面角.
的平面角.
在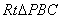 中,设
中,设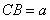 ,则
,则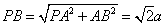 ,
,
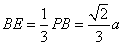 ,
,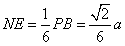 ,
,
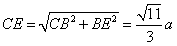 ,
,
由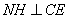 ,
,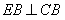 可知:
可知: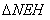 ∽
∽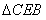 ,∴
,∴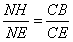 ,
,
代入解得: .
.
 在
在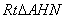 中,
中,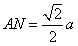 ,∴
,∴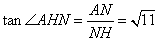 ,
,
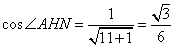 .
.
∴二面角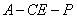 的余弦值为
的余弦值为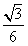 .
.
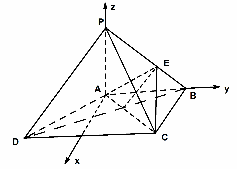
方法二:以 为原点,
为原点,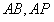 所在直线分别为
所在直线分别为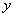 轴、
轴、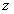 轴,如图建立空间直角坐标系.
轴,如图建立空间直角坐标系.
设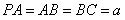 ,则
,则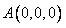 ,
,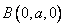 ,
,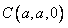 ,
,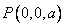 ,
,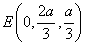 .
.
设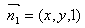 ,为平面
,为平面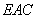 的一个法向量,则
的一个法向量,则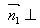
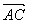 ,
,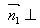
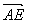 ,∴
,∴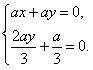 ,解得
,解得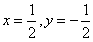 ,∴
,∴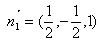 .
.
设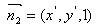 为平面
为平面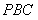 的一个法向量,则
的一个法向量,则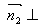
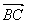 ,
,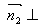
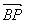 ,
,
又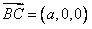 ,
, ,∴
,∴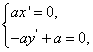 ,解得
,解得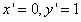 ,∴
,∴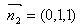 .
.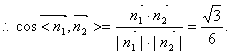 ∴二面角
∴二面角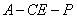 的余弦值为
的余弦值为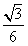 .
.
19. 解:(Ⅰ)圆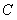 方程可化为
方程可化为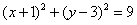 ,
,
∴圆心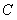 (-1,3),半径为
(-1,3),半径为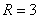 .
.
∵点P、Q在圆上且关于直线l对称,
∴圆心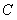 (-1,3)在直线l上.
(-1,3)在直线l上.
又直线l过点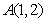 ,由两点式得
,由两点式得 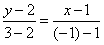
即直线l的方程为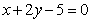
(Ⅱ)设PQ的中点为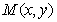 ,
,
∵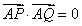 ,∴
,∴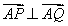
∴在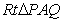 中,
中,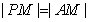 , 连结CM,则
, 连结CM,则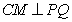 ,
,
所以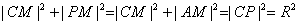 ,
,
所以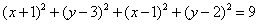
 故线段PQ中点M的轨迹方程为
故线段PQ中点M的轨迹方程为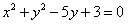 .
.
18. 证明:(Ⅰ)证:  三棱柱
三棱柱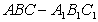 中
中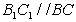 ,又
,又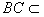 平面
平面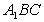 ,
,
且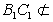 平面
平面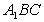 ,
,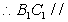 平面
平面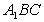
(Ⅱ)证: 三棱柱
三棱柱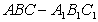 中
中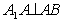 ,
,
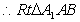 中,
中,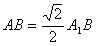 ,
,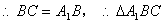 是等腰三角形.
是等腰三角形.
 E是等腰
E是等腰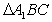 底边
底边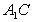 的中点,
的中点,
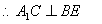 ①
①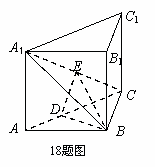
又依条件知 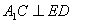 ②
②
且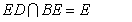 ③
③
由①,②,③得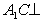 平面EDB.
平面EDB.
17. 解:
|
题目 |
测量底部不能到达的烟囱的高 |
计算过程 |
|||
|
测 量 数 据 |
测量项目 |
第一次 |
第二次 |
平均值 |
 |
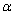 |
74°52' |
75°8' |
75° |
||
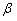 |
30°12' |
29°48' |
30° |
||
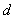 ( (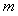 ) ) |
59.78 |
60.22 |
60 |
||
|
测量目标 (附图) |
 |
||||
|
结果 |
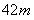 |
13. 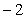 14.
14. 15.
15.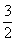 16.①②③
16.①②③
1. D 2.C 3.B 4. A 5.C 6. B 7. B 8. D 9.D 10. A 11. D 12.B
22. (本题满分12分)已知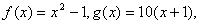 各项均为正数的数列
各项均为正数的数列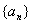 满足
满足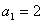 ,
, ,
, 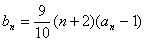 .
.
(Ⅰ)求证:数列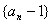 是等比数列;
是等比数列;
(Ⅱ)当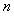 取何值时,
取何值时,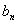 取最大值,并求出最大值;
取最大值,并求出最大值;
(Ⅲ)若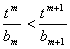 对任意
对任意 恒成立,求实数
恒成立,求实数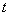 的取值范围.
的取值范围.
21.(本题满分12分)已知函数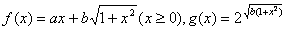 ,且
,且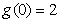 ,
,
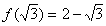 .
.
(Ⅰ)求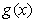 的值域;
的值域;
(Ⅱ)指出函数 的单调性(不需证明),并求解关于实数
的单调性(不需证明),并求解关于实数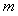 的不等式
的不等式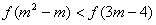 ;
;
(Ⅲ)定义在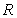 上的函数
上的函数 满足
满足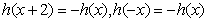 ,且当
,且当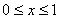 时
时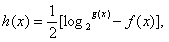 求方程
求方程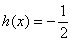 在区间
在区间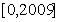 上的解的个数.
上的解的个数.
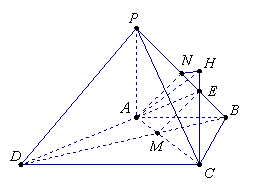
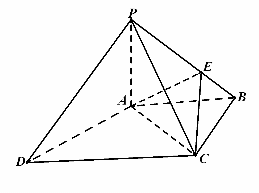
20. (本题满分12分)如图,四棱锥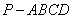 中,
中,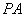 ⊥底面
⊥底面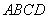 ,底面
,底面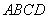 为梯形,
为梯形,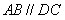 ,
,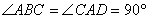 ,且
,且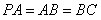 ,点
,点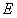 是棱
是棱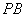 上的动点.
上的动点.
(Ⅰ)当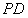 ∥平面
∥平面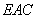 时,确定点
时,确定点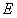 在棱
在棱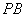 上的位置;
上的位置;
(Ⅱ)在(Ⅰ)的条件下,求二面角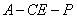 余弦值.
余弦值.
19. (本题满分12分)已知圆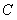 :
: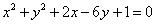 内一定点
内一定点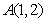 , P、Q为圆上的动点.
, P、Q为圆上的动点.
(Ⅰ)若P、Q两点关于过定点A的直线l对称,求直线l的方程;
(Ⅱ)若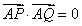 ,求线段PQ中点M的轨迹方程.
,求线段PQ中点M的轨迹方程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com