
8.过定点P(0,2)作直线l,使l与曲线y2=4(x-1)有且仅有1个公共点,这样的直线l共有( )
A.1条 B.2条 C.3条 D.4条
7.抛物线y2=2px与y2=2q(x+h)有共同的焦点,则p、q、h之间的关系是( )
A.2h=q-p B.p=q+2h C.q>p>h D.p>q>h
6.中心在原点,焦点坐标为(0,
±5 )的椭圆被直线3x-y-2=0截得的弦的中点的横坐标为
)的椭圆被直线3x-y-2=0截得的弦的中点的横坐标为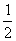 ,则椭圆方程为( )
,则椭圆方程为( )
A.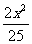 +
+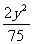 =1 B.
=1 B.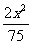 +
+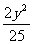 =1
=1
C.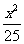 +
+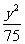 =1 D.
=1 D.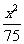 +
+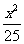 =1
=1
5.方程y2=ax+b与y=ax+b(a≠0)表示的图形可能是( )
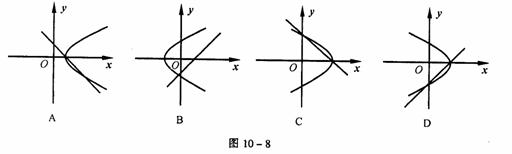
4.以原点为顶点,椭圆C: +
+ =1的左准线为准线的抛物线交椭圆C的右准线于A、B两点,则|AB|等于( )
=1的左准线为准线的抛物线交椭圆C的右准线于A、B两点,则|AB|等于( )
A.2 B.4 C.8 D.16
3.双曲线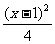 -
-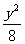 =1的渐近线方程是( )
=1的渐近线方程是( )
A.y=±2x B.y=± x C.y=±2(x-1) D.y=±
x C.y=±2(x-1) D.y=± (x-1)
(x-1)
2.椭圆x2+5y2-4x+10y+4=0的准线方程是( )
A.x=±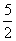 B.x= -
B.x= -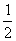 ,x=
,x=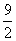
C.x= -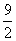 ,x=
,x=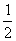 D.x= -
D.x= - ,x=
,x=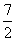
1.到定点的距离与到定直线的距离之比等于log23的点的轨迹是( )
A.圆 B.椭圆 C.双曲线 D.抛物线
3.避免繁复运算的基本方法可以概括为:回避,选择,寻求。所谓回避,就是根据题设的几何特征,灵活运用曲线的有关定义、性质等,从而避免化简方程、求交点、解方程等繁复的运算。所谓选择,就是选择合适的公式,合适的参变量,合适的坐标系等,一般以直接性和间接性为基本原则。因为对普通方程运算复杂的问题,用参数方程可能会简单;在某一直角坐标系下运算复杂的问题,通过移轴可能会简单;在直角坐标系下运算复杂的问题,在极坐标系下可能会简单“所谓寻求”。
[例题解析]
例1 设直线l:x=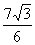 ,定点A(
,定点A( ,0),动点P到直线l的距离为d,且
,0),动点P到直线l的距离为d,且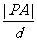 =
=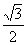 。求动点P的轨迹C的方程。
。求动点P的轨迹C的方程。
解 设动点P(x,y)。由题意得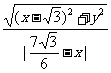 =
=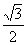 ,
,
由两边平方得,x2-2 x+3+y2=
x+3+y2=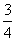 (x2-
(x2-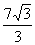 x+
x+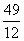 ),
),
即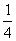 x2 -
x2 - 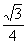 x+y2=
x+y2=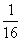 。
。
经配方得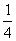 (x-
(x-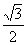 )2+y2=
)2+y2=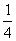 ,即(x-
,即(x-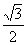 )2+
)2+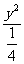 =1。
=1。
例2 已知抛物线C的对称轴与y轴平行,顶点到原点的距离为5。若将抛物线C向上平移3个单位,则在x轴上截得的线段长为原抛物线C在x轴上截得的线段长的一半;若将抛物线C向左平移1个单位,则所得抛物线过原点,求抛物线C的方程。
解 设所求抛物线方程为(x-h)2=a(y-k)(a∈R,a≠0) ①
由①的顶点到原点的距离为5,得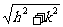 =5 ②
=5 ②
在①中,令y=0,得x2-2hx+h2+ak=0。设方程的二根为x1,x2,则
|x1-x2|=2 。
。
将抛物线①向上平移3个单位,得抛物线的方程为
(x-h)2=a(y-k-3)
令y=0,得x2-2hx+h2+ak+3a=0。设方程的二根为x3,x4,则
|x3-x4|=2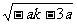 。
。
依题意得2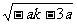 =
=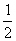 ·2
·2 ,
,
即 4(ak+3a)=ak ③
将抛物线①向左平移1个单位,得(x-h+1)2=a(y-k),
由抛物线过原点,得(1-h)2=-ak ④
由②③④得a=1,h=3,k=-4或a=4,h=-3,k=-4。
∴所求抛物线方程为(x-3)2=y+4,或(x+3)2=4(y+4)。
例3 设椭圆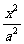 +
+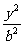 =1的两焦点为F1、F2,长轴两端点为A1、A2。
=1的两焦点为F1、F2,长轴两端点为A1、A2。
(1)P是椭圆上一点,且∠F1PF2=60°,求△F1PF2的面积;
(2)若椭圆上存在一点Q,使∠A1QA2=120°,求椭圆离心率e的取值范围。
解 (1)设|PF1|=r1,|PF2|=r2,则r1+r2=2a。
在△F1PF2中,|F1F2|=2c, ∠F1PF2=60°,
由余弦定理,得4c2=r12+r22 –2r1r2cos60°=(r1+r2)2 –3r1r2,
将r1+r2=2a代入,得r1r2=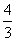 (a2-c2)=
(a2-c2)= 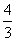 b2
b2
∴S△F PF
PF =
=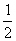 r1r2sin60°
r1r2sin60°
=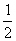 ·
·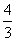 b2·
b2·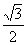 =
=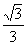 b2。
b2。
(2)设点Q的坐标为(x0,y0),则b2x02+a2y02=a2b2。
∵∠A1QA2=120°,又不妨设A1(a,0),A2(-a,0),
∴tan(π-∠A1QA2)=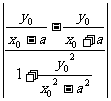 =
=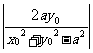 =
=
将x02=a2 -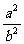 y02代入得
y02代入得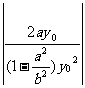 =
= 解得,y0=
解得,y0=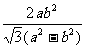
∵-b≤y0≤b ∴ b2+2ab -
b2+2ab - a2≤0
a2≤0
即 (
(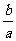 )2+2(
)2+2(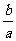 )-
)- ≤0,解得
≤0,解得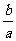 ≤
≤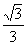 ,e2=1-
,e2=1-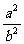 ≥
≥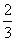 ,且e2<1。∴
,且e2<1。∴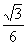 ≤e<1。
≤e<1。
例4 设双曲线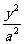 -
-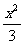 =1的焦点分别为F1、F2,离心率为2。
=1的焦点分别为F1、F2,离心率为2。
(1)求此双曲线的渐近线L1、L2的方程;
(2)若A、B分别为L1、L2上的动点,且2|AB|=5|F1F2|,求线段AB的中点M的轨迹方程并说明轨迹是什么曲线。
解 (1)由已知得已知双曲线的离心率为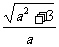 =2,解得a2=1,所以已知双曲线方程为y2-
=2,解得a2=1,所以已知双曲线方程为y2-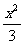 =1,它的渐近线L1、L2的方程为x-
=1,它的渐近线L1、L2的方程为x- y=0和x+
y=0和x+ y=0。
y=0。
(2)因为|F1F2|=4,2|AB|=5|F1F2|,所以|AB|=10。
设A在L1上,B在L2上,则可以设A( y1,y1)、B(-
y1,y1)、B(- y2、y2),
y2、y2),
∴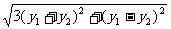 =10 ①
=10 ①
设AB的中点M(x,y),则x=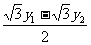 ,y=
,y=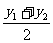 。
。
∴y1-y2=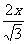 ,y1+y2=2y,
,y1+y2=2y,
代入①得12y2+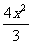 =100,即中点M的轨迹方程为
=100,即中点M的轨迹方程为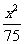 +
+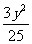 =1,是椭圆。
=1,是椭圆。
例5 已知椭圆的一个顶点为A(0,-1),焦点在x轴上,其右焦点到直线x-y+2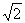 =0的距离为3,
=0的距离为3,
(1)求椭圆方程;
(2)椭圆与直线y=kx+m(k≠0)相交于不同的两点M、N,当|AM|=|AN|时,求m的取值范围。
解 (1)设已知椭圆方程为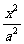 +
+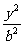 =1(a>b>0)
=1(a>b>0)
其中b=1。又设右焦点为(c,0),则
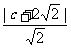 =3,解得c=
=3,解得c=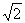 ,∴a=
,∴a= 。
。
∴椭圆方程为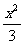 +y2=1。
+y2=1。
(2)设P为MN的中点,
解方程组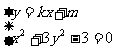 得
得
(3k2+1)x2+6mkx+3(m2-1)=0
Δ= -12m2+36k2+12>0,得m2<3k2+1 ①
又xM+xN=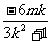 ,xP=
,xP=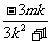
yP=kxP+m=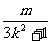 ∴kAP=
∴kAP=
又由MN⊥AP得  = -
= -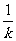 。
。
变形后,得2m=3k2+1 ②
把②代入①,得2m>m2,解得0<m<2。
又由②得k2=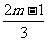 >0,解得m>
>0,解得m>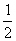 。
。
∴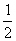 <m<2。
<m<2。
例6 已知曲线C:x2-y2=1及直线L:y=kx-1,曲线C′与C关于直线L对称。
(1)当k=1时,求曲线C′的方程;
(2)求证:不论实数k为何值,C与C′恒有公共点。
解 (1)设P(x,y)是所求曲线C′上任意一点,P点关于直线L的对称点Q(x0,y0)在已知曲线C上。
∴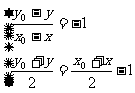 解得
解得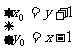
代入C的方程得(y+1)2-(x-1)2=1,即得C′的方程。
(2)①当C与C′有公共点且在L上时,此公共点也即是C与L的公共点。
∴方程组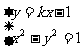 有实数解,
有实数解,
∴方程x2-(kx-1)2=1有实根,
∴(1-k2)x2+2kx-2=0有实根。
当k2=1,即k=±1时,方程有实根x=±1,C与L有两个公共点;
当k2≠1,即k≠±1时,△=4k2+8(1-k2) ≥0,
解得-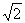 ≤k≤
≤k≤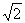 ,且k≠±1。
,且k≠±1。
∴当-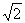 ≤k≤
≤k≤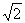 时,C与L有公共点,C与C′也有公共点。
时,C与L有公共点,C与C′也有公共点。
②当C与C′的公共点P不在L上时,则P点关于L的对称点Q也是C与C′的公共点,所以P、Q两点均在C上,
即C上有不同两点P、Q关于L对称。
设P、Q所在直线的方程是y= - 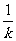 x+b(k≠0)。
x+b(k≠0)。
由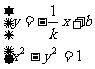 消去y得
消去y得
(1-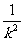 )x2+
)x2+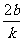 x-b2-1=0
x-b2-1=0
∴△=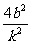 +4(b2+1)(1-
+4(b2+1)(1-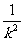 )>0 (1)
)>0 (1)
又PQ的中点M(xM,yM)在L上,
且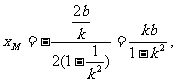
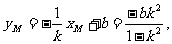
∴将xM、yM代入L的方程得
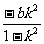 =
=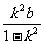 -1,即b=
-1,即b=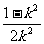 ,
,
代入(1)式解得:k∈(-∞,-1)∪(-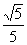 ,0)∪(0,
,0)∪(0, 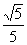 )∪(1,+∞)。
)∪(1,+∞)。
∴k∈(-∞,-1)∪(-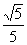 ,0)∪(0,
,0)∪(0, 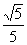 )∪(1,+∞)时,C与C′有不在L上的公共点。
)∪(1,+∞)时,C与C′有不在L上的公共点。
由于①与②中,k的解集的并集为实数集R,∴不论实数k为何值,C与C′恒有公共点。
例7 已知椭圆C的方程为x2+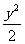 =1,点P(a,b)的坐标满足a2+
=1,点P(a,b)的坐标满足a2+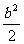 ≤1。过点P的直线l与椭圆交于A、B两点,点Q为线段AB的中点,求:
≤1。过点P的直线l与椭圆交于A、B两点,点Q为线段AB的中点,求:
(1)点Q的轨迹方程;
(2)点Q的轨迹与坐标轴的交点的个数。
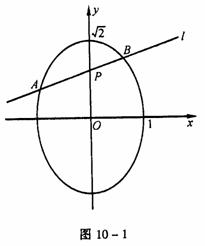
解 (1)设点A、B的坐标分别为A(x1,y1)、B(x2,y2),点Q的坐标为(x,y)。当x1≠x2时,设直线l的斜率为k,则l的方程为y=k(x-a)+b。
又已知x12+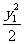 =1,x22+
=1,x22+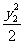 =1 ①
=1 ①
y1=k(x1-a)+b,y2=k(x2-a)+b ②
∴由①得
(x1+x2)(x1-x2)+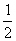 (y1+y2)(y1-y2)=0 ③
(y1+y2)(y1-y2)=0 ③
由②得
y1+ y2=k(x1+x2)-2ak+2b ④
∴由③、④及x=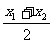 ,y=
,y=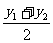 ,k=
,k=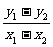
得点Q的坐标满足方程
2x2+y2-2ax-by=0 ⑤
当x1=x2时,k不存在,此时l平行于y轴,因此AB的中点Q一定落在x轴上,即Q的坐标为(a,0)。显然点Q的坐标满足方程⑤。
综上所述,点Q的坐标满足方程
2x2+y2-2ax-by=0
设方程⑤所表示的曲线为L,
则由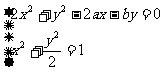
得(2a2+b2)x2-4ax+2-b2=0
因为Δ=8b2(a2+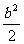 -1),又已知a2+
-1),又已知a2+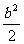 ≤1,
≤1,
所以当a2+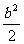 =1时,△=0,曲线L与椭圆C有且只有一个交点P(a,b)。
=1时,△=0,曲线L与椭圆C有且只有一个交点P(a,b)。
当a2+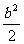 <1时,△<0,曲线L与椭圆没有交点。
<1时,△<0,曲线L与椭圆没有交点。
因为(0,0)在椭圆C内,又在曲线L上,所以曲线L在椭圆内。
故点Q的轨迹方程为2x2+y2-2ax-by=0(-1≤x≤1)。
(2)由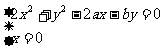 解得曲线L与y轴交于点(0,0),(0,b)。
解得曲线L与y轴交于点(0,0),(0,b)。
由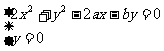 解得曲线L与x轴交于点(0,0),(a,0)。
解得曲线L与x轴交于点(0,0),(a,0)。
当a=0,b=0,即点P(a,b)为原点时,(a,0)、(0,b)与(0,0)重合,曲线L与坐标轴只有一个交点(0,0)。
当a=0,且0<|b|≤1,即点P(a,b)不在椭圆C外且在除去原点的y轴上时,曲线L与坐标轴有两个交点(0,b)与(0,0)。
同理,当b=0且0<|a|≤1时,曲线成坐标轴有两个交点(a,0),(0,0)。当0<|a|≤1,0<|b|≤1,即点P(a,b)不在椭圆C外且不在坐标轴上时,曲线L与坐标有三个交点(a,0)、(0,b)与(0,0)。
例8 在直角坐标系中,△ABC的两个顶点C、A的坐标分别为(0,0)、(2 ,0),三个内角A、B、C满足2sinB=
,0),三个内角A、B、C满足2sinB= (sinA+sinC)。
(sinA+sinC)。
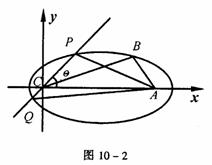
(1)求顶点B的轨迹方程;
(2)过顶点C作倾斜角为θ的直线与顶点B的轨迹交于P、Q两点,当θ∈(0, 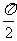 )时,求△APQ面积S(θ)的最大值。
)时,求△APQ面积S(θ)的最大值。
解 (1)设△ABC的三个内角A、B、C所对的边分别为a、b、c。
由正弦定理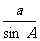 =
=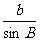 =
=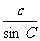 =2R。
=2R。
∵2sinB= (sinA+sinC)
(sinA+sinC)
∴2b= (a+c)
(a+c)
∵b=2
∴a+c=4
即|BC|+|BA|=4.
由椭圆定义知,B点轨迹是以C、A为焦点,长轴长为4,中心在( ,0)的椭圆。
,0)的椭圆。
∴B点轨迹方程为
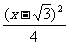 +y2=1(y≠0)
+y2=1(y≠0)
(2)设直线PQ的方程为y=x·tanθ,θ∈(0,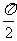 ),
),
由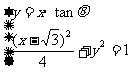
得(1+4tan2θ)x2 -2 x-1=0。
x-1=0。
设方程两根为x1、x2,
则x1+x2=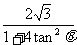 , x1·x2=
, x1·x2=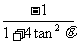
∴|PQ|=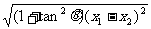
=
=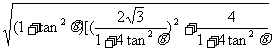
=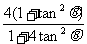
∵点A到直线PQ的距离d=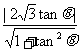 =
=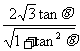 ,
,
(∵θ∈(0, 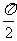 ), ∴tanθ>0)
), ∴tanθ>0)
∴S(θ)= 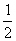 |PQ|·d
|PQ|·d
=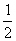 ·
·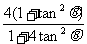 ·
·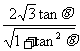
=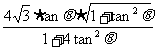
=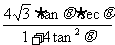
=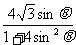
=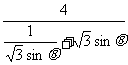 ≤2
≤2
当且仅当 sinθ=
sinθ=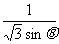 时,
时,
即sinθ=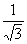 ,θ=arcsin
,θ=arcsin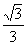 时,等号成立。
时,等号成立。
∴s(θ)的最大值为2。
例9 设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A、B两点,点C在抛物线的准线上,且BC∥x轴。证明直线AC经过原点O(2001年全国高考数学试题)
证明一 如图10-4,因为抛物线y2=2px(p>0)的焦点为F(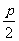 ,0),
,0),
所以经过点F的直线AB的方程可设为x=my+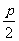 ;
;
代入抛物线方程得y2-2pmy-p2=0。
若记A(x1,y1),B(x2,y2),则y1,y2是该方程的两个根,所以y1y2=
-p2。因为BC∥x轴,且点C在准线x= -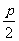 上,所以点C的坐标为(-
上,所以点C的坐标为(-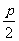 ,y2),
,y2),
故直线CO的斜率为k=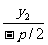 =
=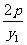 =
=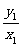 。
。
即k也是直线OA的斜率,所以直线AC经过原点O 。
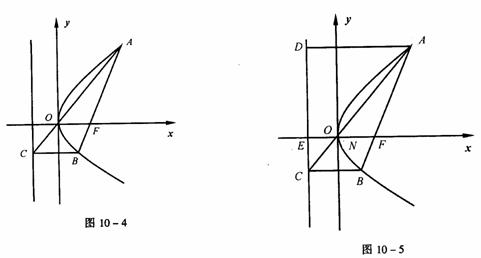
证明二 如图10-5,记x轴与抛物线准线l的交点为E,过A作AD⊥l,D是垂足,则AD∥FE∥BC。连结AC,与EF相交于点N,则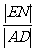 =
=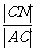 =
= ,
,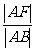 =
=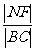 ,根据抛物线的几何性质,|AF|=|AD|,|BF|=|BC|,∴|EN|=
,根据抛物线的几何性质,|AF|=|AD|,|BF|=|BC|,∴|EN|=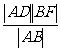 =
=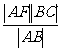 =|NF|,即点N是EF的中点,与抛物线顶点O重合,所以直线AC经过原点O。
=|NF|,即点N是EF的中点,与抛物线顶点O重合,所以直线AC经过原点O。
例10如图10-6,已知梯形ABCD中|AB|=2|CD|,点E分有向线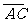 所成的比例为λ,双曲线过C、D、E三点,且以A、B为焦点。当
所成的比例为λ,双曲线过C、D、E三点,且以A、B为焦点。当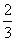 ≤λ≤
≤λ≤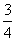 时,求双曲线离心率e的取值范围(2000年全国高考数学试题)。
时,求双曲线离心率e的取值范围(2000年全国高考数学试题)。
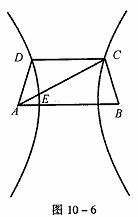
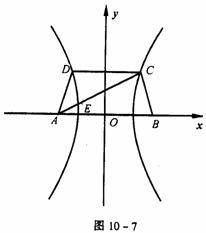
解 如图10-7,以AB的垂直平分线为y轴,直线AB为x轴,建立直角坐标系xOy,则CD⊥y轴。因为双曲线经过点C、D,且以A、B为焦点,由双曲线的对称性知C、D关于y轴对称。依题意,记A(-c,0),C(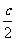 ,h),E(x0,y0),其中c=
,h),E(x0,y0),其中c=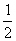 |AB|为双曲线的半焦距,h是梯形的高。
|AB|为双曲线的半焦距,h是梯形的高。
由定比分点坐标公式得
x0=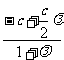 =
=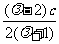 ,y0=
,y0=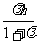
设双曲线的方程为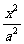 -
-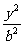 =1,则离心率e=
=1,则离心率e=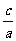 。
。
由点C、E在双曲线上,将点C、E的坐标和e=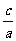 代入双曲线方程得
代入双曲线方程得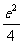 -
-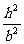 =1 ①
=1 ①
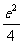 (
(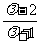 )2-(
)2-(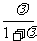 )2
)2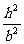 =1 ②
=1 ②
由①式得 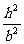 =
=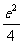 -1
③
-1
③
将③式代入②式,整理得 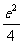 (4-4λ)=1+2λ,故λ=1-
(4-4λ)=1+2λ,故λ=1-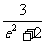 。由题设
。由题设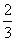 ≤λ≤
≤λ≤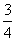 得,
得,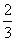 ≤1-
≤1-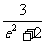 ≤
≤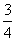 ,解得
,解得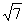 ≤e≤
≤e≤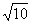 。所以双曲线的离心率的取值范围为[
。所以双曲线的离心率的取值范围为[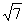 ,
,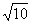 ]。
]。
2.本节解题时用到的主要数学思想方法有:
(1)函数方程思想。求平面曲线的轨迹方程,其解决问题的最终落脚点就是将几何条件(性质)表示为动点坐标x、y的方程或函数关系(参数法)。
(2)数形结合思想。解题时重视方程的几何意义和图形的辅助作用是非常必要的。即将对几何图形的研究,转化为对代数式的研究,同时又要理解代数问题的几何意义。
(3)等价转化思想。在解决问题的过程中往往需要将一个问题等价转化为另一个较为简单的问题去求解。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com