∴　所求二面角C－AB₁－A₁的大小为p－arctan2． ……………………………8分

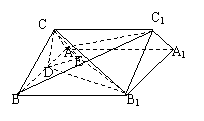
　　（3）解：连结BC₁，

　　∵　       BB₁CC₁是菱形　∴　BC₁⊥B₁C.

　　∴　CD⊥平面ABB₁A₁，B₁D⊥AB，　∴　B₁C⊥AB，

　　∴　B₁C⊥平面ABC₁，　∴　B₁C⊥C₁A．      ……………………………12分

∴　tan∠CED＝＝2．　

18．解析：（1）如图，在平面ABB₁A₁内，过B₁作B₁D⊥AB于D，

　　∵　侧面ABB₁A₁⊥平面ABC，

∴　B₁D⊥平面ABC，∠B₁BA是B₁B与平面ABC所成的角，

∴　∠B₁BA＝60°．               ……………………………2分

　　∵　四边形AB B₁A₁是菱形，

　　∴　△AB B₁为正三角形，

　　∴　D是AB的中点，即B₁在平面ABC上的射影为AB的中点．…………………4分

　　（2）连结CD，∵　△ABC为正三角形，

　　又∵　平面ABB₁A₁⊥平面ABC，平面ABB₁A₁∩平面ABC＝AB，

∴　CD⊥平面ABB₁A₁，在平面ABB₁A₁内，过D作DE⊥A₁B于E，

连结CE，则CE⊥A₁B，

∴　∠CED为二面角C- AB₁-B的平面角．　　　　　 ……………………………6分

在Rt△CED中，CD＝2sin60° ＝，

连结A₁B于O，则BO＝，DE＝BO＝，

　　∵　3＋a＝4，∴　a＝1，此时x＝．                ……………………………12分

17．解：（1）f (x)＝sin2x＋cos2x＋1＋a＝2sin(2x＋)＋1＋a．…………………………3分

　　解不等式2kp－≤2x＋≤2kp＋．

　　得kp－≤x≤kp＋　(k ÎZ)

　　∴　f (x)的单调增区间为[kp－，kp＋]  (k ÎZ)．      ……………………………6分

　　（2）∵　x Î [0，]，　∴　≤2x＋≤．          ……………………………8分

　　∴　当2x＋＝，即x＝时，f (x)_max＝3＋a．         ……………………………10分

13．7　　14．24　　　15．R(S₁＋S₂＋S₃＋S₄)　　　16．

（Ⅱ）求不等式f (x)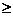kx的解集。

太  原  五  中

2006―2007学年度第二学期月考试题（5月）

高三数学答案(文)

1

2

3

4

5

6

7

8

9

10

11

12

C

B

C

B

A

C

C

D

D

C

D

B

22.（12分）定义在R上的函数 f (x)=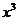 +a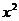+bx（a，b为常数），在x= -1处取得极值，且f (x)的图象在P（1，f (1)）处的切线平行直线y=8x，

（Ⅰ）求函数f (x)的解析式及极值；

（Ⅱ）当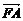=λ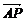时，求λ的最大值.

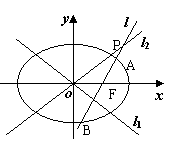（Ⅰ）当l₁与l₂夹角为60°，双曲线的焦距为4时，求椭圆C的方程；