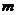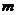解得= 2，= - 8(舍去) .

∴ P（2，4）.                     

∴ .

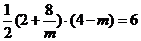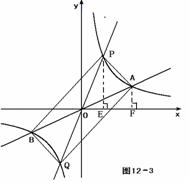
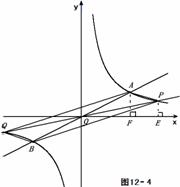
若0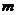＜＜4，如图12-3，

∵ S_△POE + S_梯形PEFA = S_△POA + S_△AOF,

∴ S_梯形PEFA = S_△POA = 6 .

过点P、A分别做轴的垂线，垂足为E、F，

∵ 点P、A在双曲线上，∴S_△POE = S_△AOF  = 4 .

得P ( ,   ) .

设点P的横坐标为（ > 0且）,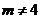

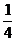∴ S_△POA =  S_{平行四边形APBQ} =   ×24 = 6  .

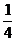∴ 四边形APBQ是平行四边形 .

∵ S_梯形CEFA = ×（2+8）×3 = 15 ,   

∴ S_△COA = 15 .                      

（3）∵ 反比例函数图象是关于原点O的中心对称图形 ,

∴ OP=OQ，OA=OB .

∵ 点C、A都在双曲线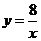上 ,

∴ S_△COE = S_△AOF  = 4  _。                             

∴ S_△COE + S_梯形CEFA = S_△COA + S_{△AOF .}

∴ S_△COA = S_{梯形CEFA  .}