
17.(本小题满分13分)已知函数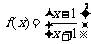 (其中x≥1).
(其中x≥1).
(1)求函数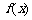 的反函数
的反函数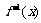 ;
;
(2)设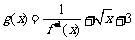 ,求函数
,求函数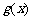 最小值及相应的x值;
最小值及相应的x值;
(3)若不等式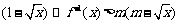 对于区间
对于区间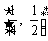 上的每一个x值都成立,求实数m的取值范围.
上的每一个x值都成立,求实数m的取值范围.
19.解析:(1)由题知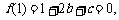
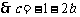
记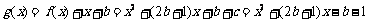 ,
,
则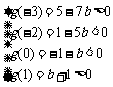
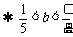 , 即
, 即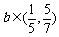 .
.
(2)令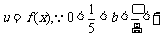 ,
, 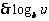 在区间
在区间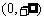 上是减函数.
上是减函数.
而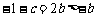 ,函数
,函数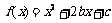 的对称轴为
的对称轴为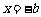 ,
,
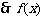 在区间
在区间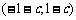 上单调递增.
上单调递增.
从而函数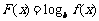 在区间
在区间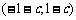 上为减函数.
上为减函数.
且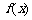 在区间
在区间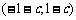 上恒有
上恒有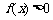 ,只需要
,只需要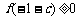 ,
,
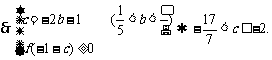
16.(本小题满分12分)已知二次函数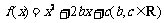 满足
满足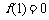 ,且关于
,且关于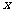 的方程
的方程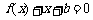 的两个实数根分别在区间
的两个实数根分别在区间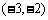 、
、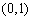 内.
内.
(1)求实数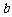 的取值范围;
的取值范围;
(2)若函数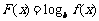 在区间
在区间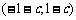 上具有单调性,求实数
上具有单调性,求实数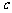 的取值范围.
的取值范围.
15.①②③
解析:由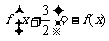 得半周期
得半周期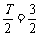 ,则
,则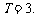 ①为真命题;
①为真命题;
由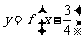 为奇函数得
为奇函数得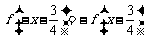 ,则
,则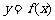 的图象关于点
的图象关于点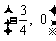 对称;②为真命题;
对称;②为真命题;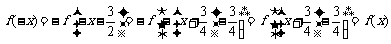 ,
,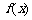 为偶函数,③为真命题;④必为假命题. 故填①②③.
为偶函数,③为真命题;④必为假命题. 故填①②③.
15.已知定义在R上的函数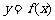 满足条件
满足条件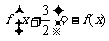 ,且函数
,且函数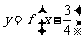 是奇函数,给出以下四个命题:
是奇函数,给出以下四个命题:
①函数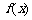 是周期函数;
是周期函数;
②函数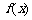 的图象关于点
的图象关于点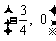 对称;
对称;
③函数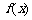 是偶函数;
是偶函数;
④函数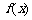 在R上是单调函数.
在R上是单调函数.
在上述四个命题中,真命题的序号是___________(写出所有真命题的序号)。
14.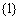 解析:
解析: ,值域为
,值域为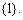
14. 函数
函数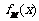 的定义域为R,且定义如下:
的定义域为R,且定义如下: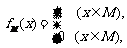 (其中M为非空数集且M R),在实数集R上有两个非空真子集A、B满足
(其中M为非空数集且M R),在实数集R上有两个非空真子集A、B满足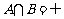 ,则函数
,则函数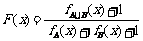 的值域为___________.
的值域为___________.
13.9;15 解析:52的“分裂”为
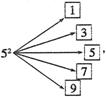
其中最大的数为9,m3的分裂数的个数构成211为首项,2为公差且项数为m的等差数列,其m项的和即为m3,则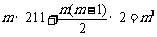 ,
,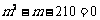 ,
,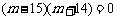 ,
,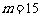 ,故填9;15.
,故填9;15.
13.如下图,对大于或等于2的自然数m的n次幂进行如下方式的“分裂”:
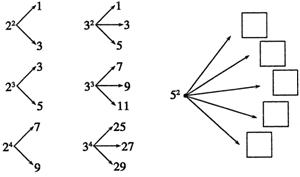
仿此,52的“分裂”中最大的数是___________,若m3的“分裂”中最小的数是211,则m的值为___________.
12.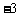 解析:∵
解析:∵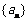 是等差数列,设公差为d,
是等差数列,设公差为d,
则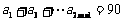 ①
① 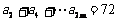 ② ①-②:
② ①-②: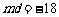 ③
③
又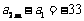 ∴
∴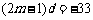 ④ 由③④得
④ 由③④得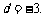
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com