（可以利用公式sinx+siny=2sin）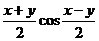

(Ⅰ)判断f 1(x)= 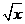, f 2(x)=x, f 3(x)= x 2中，哪些是“保三角形函数”，哪些不是，并说明理由；

(Ⅱ)如果g(x)是定义在R上的周期函数, 且值域为(0，+∞), 证明g(x)不是“保三角形函数”；

(Ⅲ)若函数F(x)=sinx, x∈(0, A)是“保三角形函数”，求A的最大值.

已知点A,B分别是射线l1:y=x(x≥0)，l2:y = -x(x≥0)上的动点, O为坐标原点，且△OAB的面积为定值2.

（Ⅰ）求线段AB中点M的轨迹C的方程;

（Ⅱ）过点N（0，2）作直线l,与曲线C交于不同的两点P,Q，与射线l1, l2分别交于点

R，S，若点P,Q恰为线段RS的两个三等分点，求此时直线l的方程.

（20）（本小题共14分）

一个函数f(x)，如果对任意一个三角形，只要它的三边长a,b,c都在f (x)的定义域内，就有f(a), f(b), f(c)也是某个三角形的三边长，则称f(x)为“保三角形函数”.

(Ⅲ)是否存在自然数n，使得S1+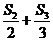+…+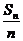=400?若存在，求n的值；若不

      存在，说明理由.

（19）(本小题共13分)

(Ⅱ)求；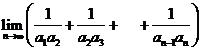

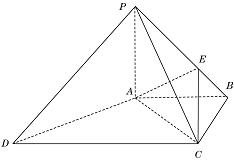如图，四棱锥P-ABCD中, PA⊥底面

ABCD,PC⊥AD.底面ABCD为梯形，

AB∥DC, AB⊥BC. PA=AB=BC, 点E在棱

PB上，且PE=2EB.

（Ⅰ）求证：平面PAB⊥平面PCB;

（Ⅱ）求证：PD∥平面EAC;

（Ⅲ）求二面角A-EC-P的大小.

（18）（本小题共14分）

设数列{an}的前n项和为Sn，已知a1=1,Sn = nan - 2n(n-1) (n=1，2，3…).

(Ⅰ)求证：数列{an}为等差数列，并分别写出an和Sn关于n的表达式;

an=Asin(ωn+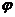)+B的通项公式，其中A，B，ω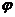，均为实数，且A>0, ω>0, |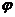|< 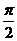, 则

此通项公式可以为an=                 （写出一个即可）.

（15）(本小题共12分)

已知在△ABC中，A>B，且tanA与tanB是方程x2-5x+6=0的两个根.

             （Ⅰ）求tan(A+B)的值；

（Ⅱ）若AB=5，求BC的长.

（16） (本小题共13分)

袋中装有大小相同的2个白球和3个黑球.

（Ⅰ）采取放回抽样方式，从中依次摸出两个球，求两球颜色不同的概率；

（Ⅱ）采取不放回抽样方式，从中依次摸出两个球，记ξ为摸出白球的个数，求ξ的期望和方差.

（17）(本小题共14分)

（14）数列{an}满足：a1=2,an=1-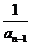(n=2，3，4，…)，则a4=       ；若{an}有一个形如

ab=     ；函数f(x)=ax3+bx, x∈[-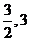]的值域为           .

（11）在北纬60°圈上有A，B两地，它们在此纬度圈上的弧长等于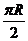(R是地球的半径)，则A，

B两地的球面距离为            .

（12）若向量a,b满足：(a-b)?(2a+b)=-4，且|a|=2,|b|=4，则a与b的夹角等于

                       .

（13）已知点P（2，2）在曲线y=ax3+bx上.如果该曲线在点P处切线的斜率为9，那么