（Ⅱ）设A（3，0），M、N 是椭圆 C 上关于 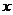 轴对称的任意两点，连结 AN 交椭圆于另一点 E，求证直线 ME 与  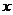轴相交于定点．

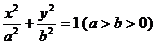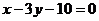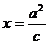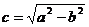已知椭圆C： 的中心关于直线  的对称点落在直线 （其中）上，且椭圆 C 的离心率为 ．

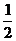（Ⅰ）求椭圆 C 的方程；

（Ⅱ）若已知当 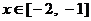 时，不等式 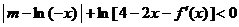 恒成立，求 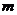 的取值范围．

（21）（本小题满分12分）

（Ⅰ）求出函数 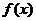 的表达式和单调区间；

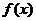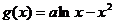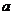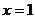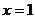已知函数  与 （ 为常数）的图象关于直线  对称，且 是 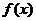 的一个极值点．

（Ⅲ）求年产量 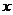 为何值时，随机变量  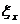的期望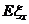 取得最大值（不需求最大值）．

（20）（本小题满分12分）

（Ⅱ）当产量 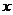 确定时，求随机变量  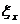的期望 ；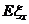

（Ⅰ）分别求利润 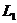、、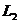 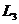与年产量 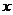 之间的函数关系式；

    设 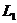、、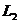 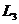分别表示市场情况好、中、差时的利润，随机变量 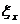 表示当年产量为  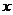而市场情况不确定时的利润．