
9、 为奇函数且
为奇函数且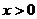 时,
时, ,当
,当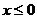 时,解析式为
时,解析式为
8、函数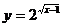 的定义域为
的定义域为 ,值域为
,值域为 。
。
7、 (05上海)若函数f(x)=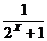 , 则该函数在(-∞,+∞)上是
( )
, 则该函数在(-∞,+∞)上是
( )
(A)单调递减无最小值 (B) 单调递减有最小值
(C)单调递增无最大值 (D) 单调递增有最大值
6、(05湖北卷)在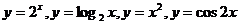 这四个函数中,当
这四个函数中,当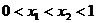 时,使
时,使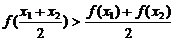 恒成立的函数的个数是( )
恒成立的函数的个数是( )
A.0 B.1 C.2 D.3
5、(04年全国卷二.文7理6)函数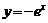 的图象(
)
的图象(
)
A.与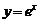 的图象关于y轴对称 B.与
的图象关于y轴对称 B.与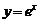 的图象关于坐标原点对称
的图象关于坐标原点对称
C.与 的图象关于y轴对称 D.与
的图象关于y轴对称 D.与 的图象关于坐标原点对称
的图象关于坐标原点对称
4、(04年全国卷一.文2)已知函数 (
)
(
)
A.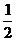 B.-
B.-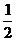 C.2 D.-2
C.2 D.-2
3、若 ,当
,当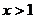 时,
时,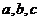 的大小关系为 ( )
的大小关系为 ( )
(A) (B)
(B)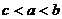 (C)
(C)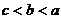 (D)
(D)
2、函数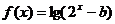 (
(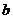 为常数),若
为常数),若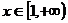 时,
时,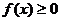 恒成立,则( )
恒成立,则( )
(A)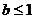 (B)
(B)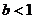 (C)
(C)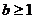 (D)
(D)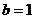
1、函数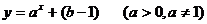 的图象不经过第二象限,则有 ( )
的图象不经过第二象限,则有 ( )
(A)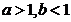 (B)
(B)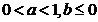 (C)
(C) (D)
(D)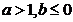
例1(1)若 ,则
( )
,则
( )
(A)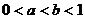 (B)
(B)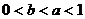 (C)
(C)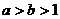 (D)
(D)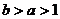
(2)函数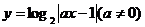 图象的对称轴为
图象的对称轴为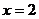 ,则
,则 为
( )
为
( )
(A)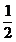 (B)
(B)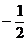 (C)
(C)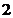 (D)
(D)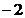
(3)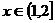 时,不等式
时,不等式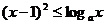 恒成立,则
恒成立,则 的取值范围是 ( )
的取值范围是 ( )
(A) (B)
(B)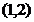 (C)
(C) (D)
(D)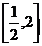
(4)已知函数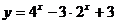 的值域为
的值域为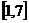 ,则
,则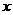 的范围是
( )
的范围是
( )
(A)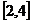 (B)
(B)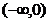 (C)
(C)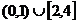 (D)
(D)
例2、比较大小
(1)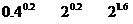 (2)
(2)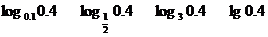
(3) 其中
其中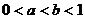
例3、要使函数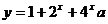 在
在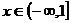 上
上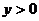 恒成立。求
恒成立。求 的取值范围。
的取值范围。
变题:设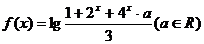 ,如果当
,如果当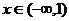 时
时 有意义,求a的取值范围。
有意义,求a的取值范围。
例4、若关于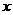 的方程
的方程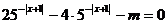 有实根,求
有实根,求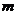 的取值范围。
的取值范围。
变题1:设有两个命题:①关于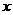 的方程
的方程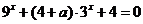 有解;②函数
有解;②函数 是减函数。当①与②至少有一个真命题时,实数
是减函数。当①与②至少有一个真命题时,实数 的取值范围是__
的取值范围是__
变题2:方程 的两根均大于1,则实数a的取值范围是_____。
的两根均大于1,则实数a的取值范围是_____。
例5、已知函数 的反函数为
的反函数为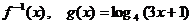
(1)
若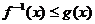 ,求
,求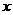 的取值范围D。
的取值范围D。
(2)
设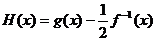 ,当
,当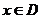 时,求函数
时,求函数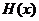 的值域
的值域
变题:已知函数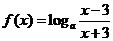 的定义域为
的定义域为 ,值域为
,值域为 ,且函数
,且函数 为
为 上的减函数,求实数
上的减函数,求实数 的取值范围。
的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com