
2.函数y=4x2+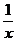 的单调增区间为…………………………………………………………(
)
的单调增区间为…………………………………………………………(
)
A.(0,+∞) B.(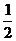 ,∞) C.(―∞,―1) D.(―∞,―
,∞) C.(―∞,―1) D.(―∞,―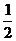 )
)
1.下列说法正确的是………………………………………………………………………( )
A.函数的极大值就是函数的最大值 B. 函数的极小值就是函数的最小值
C.函数的最值一定是极值 D.在闭区间上的连续函数一定存在最值
3、函数的最大值与最小值
在闭区间[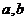 ]上连续,在(
]上连续,在(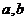 )内可导,
)内可导, 在[
在[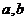 ]上求最大值与最小值的步骤:
]上求最大值与最小值的步骤:
先求  在(
在(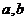 )内的极值;再将
)内的极值;再将 的各极值与
的各极值与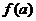 、
、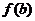 比较,其中最大的一个是最大值,最小的一个是最小值。
比较,其中最大的一个是最大值,最小的一个是最小值。
特别注意:要注意区分函数最值与极值的区别、联系。
2、函数的极值
(1)极值定义
如果函数 在点
在点 附近有定义,而且对
附近有定义,而且对 附近的点,都有
附近的点,都有 <
<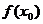 我们就说
我们就说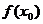 是函数的一个极大值,记作
是函数的一个极大值,记作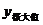 =
=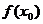 ;
;
 在点
在点 附近的点,都有
附近的点,都有 >
>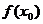 我们就说
我们就说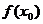 函数的一个极小值,记作
函数的一个极小值,记作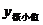 =
=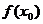 ;
;
极大值与极小值统称为极值。
(2)极值判别法
当函数 在点
在点 处连续时,极值判断法是:
处连续时,极值判断法是:
如果在 附近的左侧
附近的左侧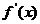 >0,右侧
>0,右侧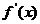 <0,那么
<0,那么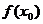 是极大值;
是极大值;
如果在 附近的左侧
附近的左侧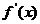 <0,右侧
<0,右侧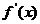 >0,那么
>0,那么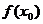 是极小值。
是极小值。
(3)求可导函数极值的步骤:
① 求导数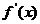 ;
;
②求导数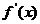 =0的根;
=0的根;
③列表,用根判断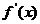 在方程根左右的值的符号,确定
在方程根左右的值的符号,确定 在这个根处取极大值还是取极小值。
在这个根处取极大值还是取极小值。
1、函数的单调性
(1)如果非常数函数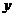 =
= 在某个区间内可导,那么若
在某个区间内可导,那么若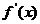
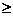 0
0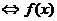 为增函数;
为增函数;
若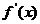
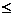 0
0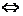
 为减函数.
为减函数.
(2)若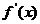
 0则
0则 为常数函数.
为常数函数.
3.搞清导数的几何意义,为解决实际问题如:切线、加速度等问题打下理论基础.
2.求函数的导数要熟练掌握求导公式,特别是复合函数的导数要学会合理地分拆。
1.函数的导数实质是一个极限问题,不应理解为平均变化率,而是平均变化率的极限
例1、用定义求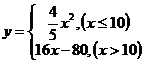 在点x=10处的导数。
在点x=10处的导数。
例2 求下列函数的导数:
(1)y=(2x2-1)(3x+1) (2)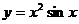 (3)
(3)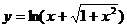
(4)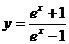 (5)
(5)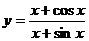 (6)
(6)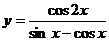
例3、已知曲线C: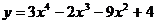
(1)求曲线C上横坐标为1的点的切线的方程;
(2)第(1)小题中切线与曲线C是否还有其它公共点。
例4(1)一球沿某一斜面自由滚下,测得滚下的垂直距离h(单位:m)与时间t(单位:s)之间的函数关系为h=t2,求t=4s时, 此球在垂直方向的瞬时速度.
(2)质点P在半径为10cm,圆心在原点的圆上逆时针做匀角速运动,角速度为1rad/s, 设该圆与x轴正半轴的交点A为起始点,求时刻t时,点P在y轴上射影点M的速度.
6.已知两曲线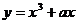 和
和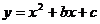 都经过点P(1,2),且在点P处有公切线,试求a,b,c值。
都经过点P(1,2),且在点P处有公切线,试求a,b,c值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com