
4.用边长为48厘米的正方形铁皮做一个无盖的铁盒时,在铁皮的四角各截去一个面积相等的小正方形,然后把四角折起,就能焊成铁盒,所做的铁盒容积最大时,在四角截去的正方形的边长为…………………………………………………………………………………( )
A.6 B.8 C.10 D.12
3.已知f(x)=(x-1)2+2,g(x)=x2-1,则f[g(x)]…………………………………………( )
A.在(-2,0)上递增
B. 在(0,2)上递增
C.在(-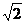 ,0)上递增 D.(0,
,0)上递增 D.(0,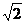 )在上递增
)在上递增
2.点M(p,p)到抛物线y2=2px的最短距离为……………………………………………( )
A.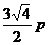 B.
B.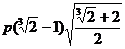 C.
C. D.以上答案都不对
D.以上答案都不对
1.下列函数存在极值的是………………………………………………………………( )
A.y=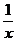 B.y=
B.y=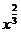 C.y=2
D.y=x3
C.y=2
D.y=x3
11. (05全国卷Ⅱ)已知a≥ 0 ,函数f(x) = ( 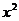 -2ax )
-2ax )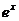
(1) 当X为何值时,f(x)取得最小值?证明你的结论;
(2)设 f(x)在[ -1,1]上是单调函数,求a的取值范围.
解:(I)对函数 求导数得
求导数得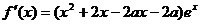
令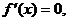 得[
得[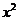 +2(1-
+2(1-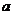 )
)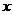 -2
-2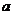 ]
]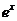 =0从而
=0从而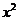 +2(1-
+2(1-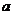 )
)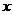 -2
-2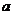 =0
=0
解得 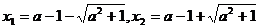
当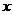 变化时,
变化时, 、
、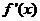 的变化如下表
的变化如下表
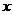 |
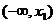 |
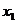 |
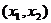 |
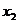 |
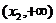 |
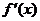 |
+ |
0 |
- |
0 |
+ |
 |
递增 |
极大值 |
递减 |
极小值 |
递增 |
∴ 在
在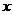 =
=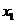 处取得极大值,在
处取得极大值,在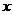 =
=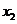 处取得极小值。
处取得极小值。
当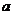 ≥0时,
≥0时,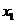 <-1,
<-1,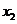
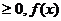 在
在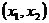 上为减函数,在
上为减函数,在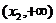 上为增函数
上为增函数
而当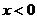 时
时 =
=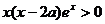 ,当x=0时,
,当x=0时,
所以当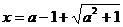 时,
时, 取得最小值
取得最小值
(II)当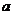 ≥0时,
≥0时, 在
在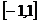 上为单调函数的充要条件是
上为单调函数的充要条件是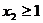
即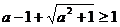 ,解得
,解得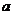

于是 在[-1,1]上为单调函数的充要条件是
在[-1,1]上为单调函数的充要条件是
即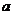 的取值范围是
的取值范围是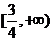
例4、已知曲线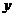 =
= =
=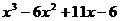 ,在它对应于
,在它对应于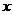
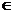 [0,2]的弧段上求一点P,使得曲线在该点的切线在
[0,2]的弧段上求一点P,使得曲线在该点的切线在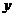 轴上的截距为最小,并求出这个最小值。
轴上的截距为最小,并求出这个最小值。
例5、设工厂A到铁路的垂直距离为20km,垂足为B,铁路线上距离B100km的地方有一个原料供应站C,现在要从BC中间某处D向工厂修一条公路,使得原料供应站C到工厂A所需运费最省。问D应选在何处?已知每一公里的铁路运费与公路运费之比为3:5。
例1、(2000年全国高考题)设函数f(x)=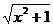 -ax,其中a>0,求a的取值范围,使函数f(x)在区间[0,+∞)上是单调函数
-ax,其中a>0,求a的取值范围,使函数f(x)在区间[0,+∞)上是单调函数
例2、偶函数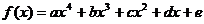 的图象过点P(0,1),且在
的图象过点P(0,1),且在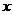 =1处的切线方程为
=1处的切线方程为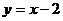 ,(1)求
,(1)求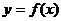 的解析式;(2)求
的解析式;(2)求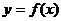 的极值。
的极值。
16.(05福建卷)已知函数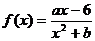 的图象在点M(-1,f(x))处的切线方程为x+2y+5=0.
的图象在点M(-1,f(x))处的切线方程为x+2y+5=0.
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)求函数y=f(x)的单调区间.
解:(1)由函数f(x)的图象在点M(-1f(-1))处的 切线方程为x+2y+5=0,知
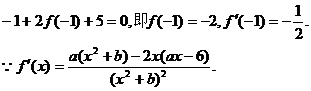
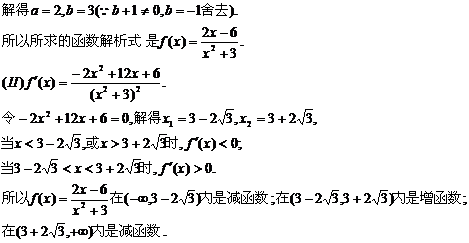
6..(04年重庆卷.理14)曲线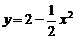 与
与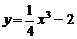 在交点处的切线夹角是 .(以弧度数作答)
在交点处的切线夹角是 .(以弧度数作答)
练3.(04年湖南卷.文13)过点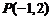 且与曲线
且与曲线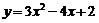 在点
在点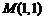 处的切线平行的直线方程是
.
处的切线平行的直线方程是
.
5.(04年全国卷二.文3)曲线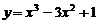 在点
在点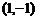 处的切线方程为( ).
处的切线方程为( ).
A. 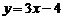 B.
B. 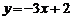 C.
C. 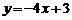 D.
D. 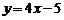
4.函数y=x4-8x2+2在[-1,3]上最大值为………………………………………………( )
A.11 B.2 C.12 D.10
3.下列说法正确的是 …………………………………………………………………… ( )
A.当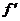 (x0)=0时,则f(x0)为f(x)的极大值 B.当
(x0)=0时,则f(x0)为f(x)的极大值 B.当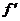 (x0)=0时,则f(x0)为f(x)的极小值
(x0)=0时,则f(x0)为f(x)的极小值
C.当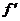 (x0)=0时,则f(x0)为f(x)的极值 D.当f(x0)为函数f(x)的极值时,则有
(x0)=0时,则f(x0)为f(x)的极值 D.当f(x0)为函数f(x)的极值时,则有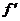 (x0)=0
(x0)=0
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com