2、某商店计划两次提价，有甲、乙、丙三种方案，(如右表，其中p>q>0.)经两次提价后，

则　　 种方案的提价幅度最大！

次 案	第一次提价	第二次提价
甲	p%	q%
乙	q%	p%
丙

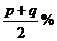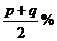1、等边圆锥母线长为8，其的内接圆柱的高为x，当内接圆柱侧面积最大时，x的值为

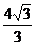(A)3　　　　　　　 (B)2　　　　 (C)　　　　　 (D)4

3.　　　 运用均值不等式求最值时，要注意是否具备使用定理的条件，即＂一正二定三等＂，三者缺一不可．

1.　　　 不等式始终贯穿在整个中学数学之中, 诸如集合问题、方程(组)的解的讨论、 函数单调性的研究、函数的定义域、值域的确定，三角、数列、复数、立体几何、解析几何中的最大值、最小值问题， 无一不与不等式有着密切关系。

12、(05湖北卷)22．(本小题满分14分)

　　　 已知不等式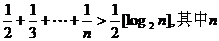为大于2的整数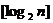，表示不超过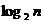的最大整数. 设数列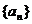的各项为正，且满足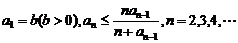

　 (Ⅰ)证明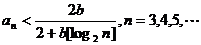

(Ⅱ)猜测数列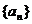是否有极限？如果有，写出极限的值(不必证明)；

(Ⅲ)试确定一个正整数N，使得当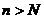时，对任意b>0，都有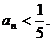

CDBDA　 BBC

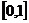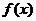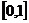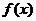10. 已知定义域为的函数同时满足:　 ①对于任意x∈,总有≥0；

②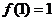； ③若x₁≥0，x₂≥0， x₁ + x₂≤0 ，则有f( x₁ + x₂)≥f( x₁)+f( x₂)

(1)求的值.　

(2)(2)求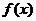的最大值.

(3)证明:满足上述条件的函数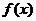对一切实数x,都有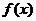≤2x.

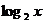*11、对满足：|p|＜2的一切p，不等式+p+1＞2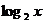+p恒成立，求实数x的取值范围(提示：可以理解为关于p的一次函数).

9. 设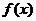是定义在R上的以3为周期的奇函数,若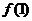>1. 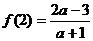.则a的取值范围是 　　　　　　　　　　　

8. 平面上的点p(x,y),使关于t的二次方程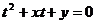的根都是绝对不超过1的实数,那么这样的点的集合在平面区域的形状是: (　 　　)

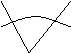
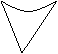
A .　　　　　　　 B.　　　　 　　　C.　　　　　　 D

7.若p=a+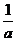+2　 (a>0)　　 q=arccost　 (－1≤t≤1) 则下列不等式恒成立的是:(　 　)

A.p≥л>q　　　　 B. p>q≥0　　　　　 C. 4>p≥q　　　　　 D. p≥q>0