
18.(本小题满分16分)已知动点 到定直线
到定直线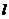 :
: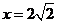 的距离与点
的距离与点 到定点
到定点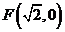 之比为
之比为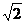 .
.
(1)求动点 的轨迹
的轨迹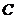 的方程;
的方程;
(2)若点N为轨迹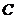 上任意一点(不在x轴上),过原点O作直线AB交(1)中轨迹C于点A、B,且直线AN、BN的斜率都存在,分别为
上任意一点(不在x轴上),过原点O作直线AB交(1)中轨迹C于点A、B,且直线AN、BN的斜率都存在,分别为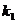 、
、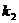 ,问
,问 是否为定值?
是否为定值?
(3)若点M为圆O: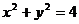 上任意一点(不在x轴上),过M作圆O的切线,交直线
上任意一点(不在x轴上),过M作圆O的切线,交直线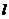 于点Q,问MF与OQ是否始终保持垂直关系?
于点Q,问MF与OQ是否始终保持垂直关系?
17.(本小题满分14分)
已知分别以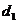 和
和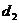 为公差的等差数列
为公差的等差数列 和
和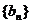 满足
满足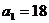 ,
,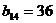 .
.
(1)若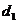 =18,且存在正整数
=18,且存在正整数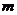 ,使得
,使得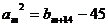 ,求证:
,求证: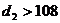 ;
;
(2)若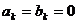 ,且数列
,且数列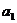 ,
,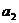 ,…,
,…, ,
,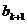 ,
, ,…,
,…,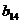 的前
的前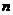 项和
项和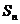 满足
满足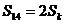 ,求数列
,求数列 和
和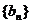 的通项公式;
的通项公式;
17解:(1)依题意,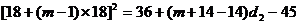 ,
,
即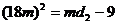 , 即
, 即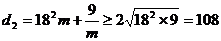 ;………4分
;………4分
等号成立的条件为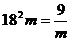 ,即
,即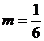 ,
,
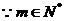 ,
,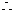 等号不成立,
等号不成立,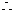 原命题成立. …………………………7分
原命题成立. …………………………7分
(2)由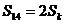 得:
得: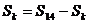 ,即:
,即: ,
,
则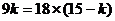 ,得
,得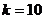 …………………………11分
…………………………11分
 ,
, , …………………………13分
, …………………………13分
则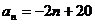 ,
,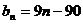 ;
………………………………14分
;
………………………………14分
16.证明:(Ⅰ)设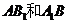 的交点为O,连接
的交点为O,连接 ,连接
,连接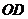 .
.
因为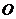 为
为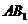 的中点,
的中点,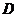 为
为 的中点,所以
的中点,所以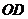 ∥
∥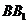 且
且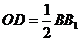 .
.
又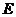 是
是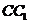 中点,
中点,
则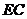 ∥
∥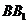 且
且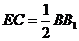 ,即
,即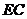 ∥
∥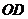 且
且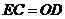 ,
,
则四边形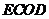 为平行四边形.所以
为平行四边形.所以 ∥
∥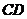 .
.
又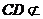 平面
平面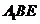 ,
,
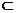 平面
平面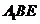 ,则
,则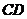 ∥平面
∥平面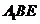 . ……………7分
. ……………7分
(Ⅱ) 因为三棱柱各侧面都是正方形,所以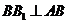 ,
,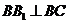 ,
,
 所以
所以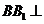 平面
平面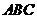 .
.
因为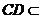 平面
平面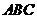 ,所以
,所以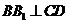 .
.
由已知得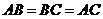 ,所以
,所以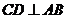 .
.
所以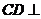 平面
平面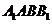 .
.
由(Ⅰ)可知 ∥
∥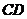 ,所以
,所以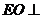 平面
平面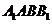 .
.
所以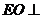
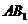 .
.
因为侧面是正方形,所以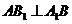 .
.
又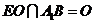 ,
,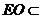 平面
平面 ,
,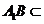 平面
平面 ,
,
所以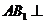 平面
平面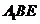 .
.
点A到到平面 ,故距离等于
,故距离等于 …………………………14分
…………………………14分
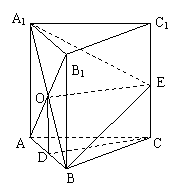
16.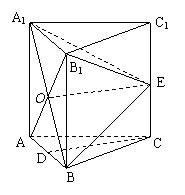 (本小题满分14分)如图,在三棱柱
(本小题满分14分)如图,在三棱柱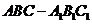 中,每个侧面均是边长为2的正方形,
中,每个侧面均是边长为2的正方形,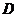 为底边
为底边 的中点,
的中点,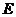 为侧棱
为侧棱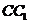 的中点,
的中点,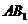 与
与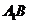 的交点为
的交点为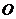 .
.
(Ⅰ)求证: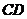 ∥平面
∥平面 ;
;
(Ⅱ)求点A到平面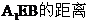 。
。
15.(本小题满分14分)
(Ⅰ)解:由三角函数的定义,得点B的坐标
为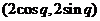 .
.
在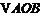 中,|OB|=2,
中,|OB|=2,
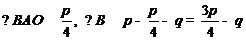 ,
,
由正弦定理,得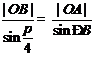 ,即
,即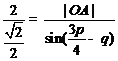 ,
,
所以 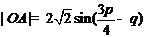 .
---------7分
.
---------7分
(Ⅱ)解:由(Ⅰ)得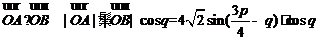 ,
,
因为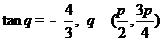 ,
,
所以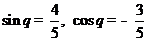 ,
----------------------------10分
,
----------------------------10分
又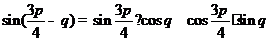
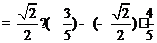
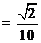 , ---------------------------12分
, ---------------------------12分
所以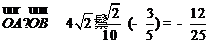 .
---------------------------14分
.
---------------------------14分
15.(本小题满分14分)
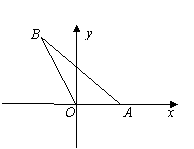 如图,在平面直角坐标系xOy中,点A在x轴正半轴上,直线AB的倾斜角为
如图,在平面直角坐标系xOy中,点A在x轴正半轴上,直线AB的倾斜角为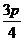 ,|OB|=2, 设
,|OB|=2, 设 .
.
(Ⅰ)用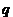 表示点B的坐标及
表示点B的坐标及 ;
;
(Ⅱ)若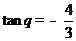 ,求
,求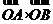 的值.
的值.
14.若存在过点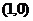 的直线与曲线
的直线与曲线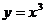 和
和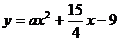 都相切,则
都相切,则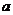 等于__▲___.
等于__▲___.
[解析]由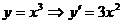 ,设曲线
,设曲线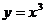 上任意一点
上任意一点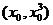 处的切线方程为
处的切线方程为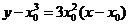 ,
,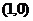 代入方程得
代入方程得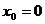 或
或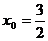
当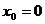 时,切线方程为
时,切线方程为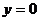 ,则
,则 ,
,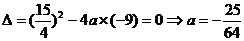
当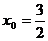 时,切线方程为
时,切线方程为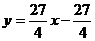 ,由
,由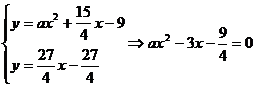 ,
,
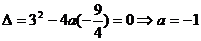 ∴
∴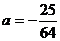 或
或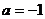 .
.
13.设点O是△ABC的外心,AB=13,AC=12,则·= ▲ .-
12.设定义在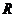 的函数
的函数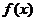 同时满足以下条件:①
同时满足以下条件:①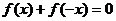 ;②
;②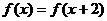 ;
;
③当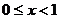 时,
时,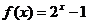 .则
.则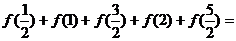 ___▲____.
___▲____.
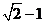
11.若对于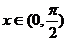 ,不等式
,不等式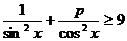 恒成立,则正实数
恒成立,则正实数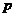 的取值范围为___▲____.
的取值范围为___▲____.
[解析]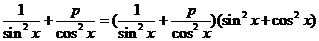
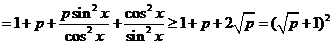
所以由不等式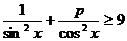 恒成立,得
恒成立,得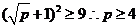
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com