
2.从某一高度相隔1s释放两个相同的小球甲和乙,不计空气阻力,它们在空中任一时刻
( )
A.甲、乙两球距离越来越大,甲、乙两球速度之差越来越大
B.甲、乙两球距离始终保持不变,甲、乙两球速度之差保持不变
C.甲、乙两球距离越来越大,但甲、乙两球速度之差保持不变
D.甲、乙两球距离越来越小,甲、乙两球速度之差越来越小
1.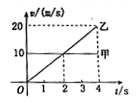 甲、乙两个质点同时、同地向同一方向做直线运动,它们的
甲、乙两个质点同时、同地向同一方向做直线运动,它们的
速度一时间图象如右图所示,则由图象可知 ( )
A.甲质点比乙质点运动得快,故乙追不上甲
B.在2s末时乙追上甲
C.在2s末时甲、乙的速度相同
D.甲做匀速直线运动,乙做初速度为零的匀加速直线运动
22.(本小题满分14分)
设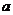 为实数,函数
为实数,函数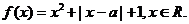
(Ⅰ)讨论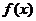 的奇偶性;
的奇偶性;
(Ⅱ)求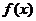 在
在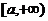 上的最小值.
上的最小值.
(Ⅲ)求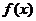 在
在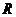 上的最小值.
上的最小值.
21.(本小题满分12分)
某市居民自来水收费标准如下:每户每月用水不超过4吨时每吨为1.80元,当用水超过4吨时,超过部分每吨3.00元,某月甲、乙两户共交水费 元,已知甲、乙两用户 该月用水量分别为
元,已知甲、乙两用户 该月用水量分别为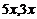 (吨)。
(吨)。
(1)求 关于
关于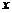 的函数;
的函数;
(2)若甲、乙两户该月共交水费26.4元,分别求出甲、乙两户该月的用水量和水费。(精确到0.1)
20.(本小题满分12分)
已知定义域为R的函数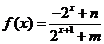 是奇函数。
是奇函数。
①求m、n的值。
②若对任意的t∈R,不等式 恒成立,求实数k的取值范围。
恒成立,求实数k的取值范围。
19.(本题满分12分)
定义在R上的函数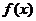 满足
满足
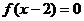 ,当
,当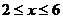 时,
时,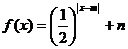 且
且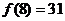
(1)求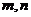 的值.
的值.
(2)比较 与
与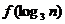 的大小
的大小
18.(本小题满分12分)
给定两个命题:
 :对任意实数
:对任意实数 都有
都有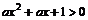 恒成立;
恒成立;
 :关于
:关于 的方程
的方程 有实数根;
有实数根;
如果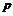 与
与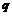 中有且仅有一个为真命题,求实数
中有且仅有一个为真命题,求实数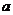 的取值范围.
的取值范围.
17.(本题满分12分)
已知全集 集合
集合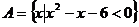 ,
,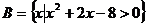 ,
, (
( )
, 若
)
, 若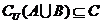 ,求实数
,求实数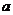 的取值范围.
的取值范围.
16.定义在R上的偶函数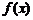 满足:
满足: ,且在
,且在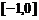 上是增函数,下面关于
上是增函数,下面关于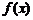 的判断:
的判断:
①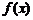 是周期函数;
是周期函数;
②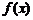 的图象关于直线
的图象关于直线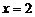 对称;
对称;
③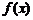 在
在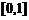 上是增函数;
上是增函数;
④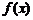 在
在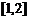 上是减函数;
上是减函数;
⑤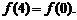
其中正确的判断的序号是 。
15.设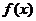 是定义在
是定义在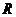 上的以3为周期的奇函数,若
上的以3为周期的奇函数,若 ,则
,则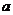 的取值范围是_________.
的取值范围是_________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com