
8.到空间不共面四点A、B、C、D距离相等的平面有(D)A.4个 B.5个 C.6个D.7个
7.三棱柱ABC-A1B1C1的体积为V,则三棱锥C1-ABB1的体积为
( C )A.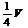 B.
B.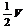 C.
C.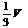 D.
D.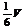
6.甲、乙两人独立地解同一问题,甲解决这个问题的概率是P1,乙解决这个问题的概率是P2,则其中至少有一个人解决这个问题的概率是 ( D )
A.P1+P2 B.P1·P2 C.1-P1·P2 D.1-(1-P1)(1-P2)
5.已知A,B,C,D是同一球面上的四点,且连接每两点的线段长都等于2,则球心到平面BCD的距离为(C )A、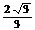 B、
B、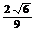 C、
C、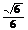 D、
D、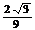
4.已知直线m、n与平面α、β,给出下列三个命题: ( C )
①若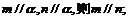 ②若
②若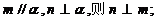
③若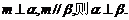 其中真命题的个数是 A.0 B.1
C.2 D.3
其中真命题的个数是 A.0 B.1
C.2 D.3
3. 在正方体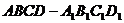 中,
中,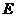 为
为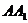 的中点,点
的中点,点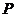 在其对角面
在其对角面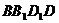 内运动,若
内运动,若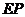 与直线
与直线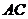 总成等角,则点
总成等角,则点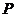 的轨迹有可能是A
的轨迹有可能是A
A.圆或圆的一部分 B.抛物线或其一部分 C. 双曲线或其一部分 D. 椭圆或其一部分
2.设地球半径为R,若甲地位于北纬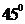 东经
东经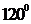 ,乙地位于南纬
,乙地位于南纬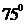 东经
东经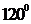 ,则甲、乙两地的球面距离为 (
D )A.
,则甲、乙两地的球面距离为 (
D )A. 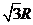 B.
B. 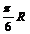 C.
C. 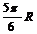 D.
D. 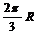
1、在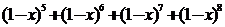 的展开式中,含
的展开式中,含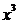 的项的系数是(D
)
的项的系数是(D
)
A.74 B.121 C.-74 D.-121
22.解法一:(1)取BC的中点H,连EH,易得EH是EF在平面AC上的射影,
∵BD⊥EH,∴由三垂线定理,得 EF⊥BD;
又∵EF在平面AB1上的射影是B1E,由△BB1E∽△ABG,得B1E⊥BG,∴由三垂线定理,得 EF⊥BG,
∵BG∩BD=B,∵EF⊥平面GBD.
(2)取C1D1的中点M,连EM,易得EM∥AD1,所以∠EFM就是异面直线AD1与EF所成的角,
∵MF∥BD,∴EF⊥MF .在Rt△EFM中,由EM=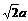 ,(a为正方体的棱长),EF=
,(a为正方体的棱长),EF= ,得
,得
∠EFM=30º.即异面直线AD1与EF所成的角为30º.
解法二:(向量法)(1) 以AD为x轴,DC为y轴,DD1为z轴建立空间坐标系,不妨设正方体的棱长为2,
则D(0,0,0),A(2,0,0),B(2,2,0),E(2,1,0),F(1,2,2),G(2,,0,1) ,D1(0,0,2 )
∵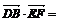 (2,2,0)·(1,-1,-2)=0,
(2,2,0)·(1,-1,-2)=0,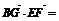 (0,-2,1)·(1,-1,-2)=0
(0,-2,1)·(1,-1,-2)=0
∴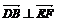 ,
,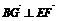 ,又∵BG∩BD=B,∵EF⊥平面GBD.
,又∵BG∩BD=B,∵EF⊥平面GBD.
(2)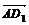 =(-2,0,2),
=(-2,0,2),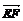 =(1,-1,-2) .
=(1,-1,-2) . 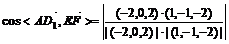 =
=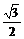 ,
,
即异面直线AD1与EF所成的角为30º.
21.解:(I)
|
正面向上次数m |
3 |
2 |
1 |
0 |
|
概率P(m) |
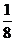 |
 |
 |
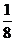 |
|
正面向上次数n |
2 |
1 |
0 |
|
概率P(n) |
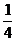 |
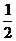 |
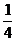 |
(II)甲获胜,则m>n,当m=3时,n=2,1,0,其概率为
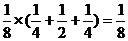
当m=2时,n=1,0. 其概率为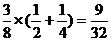
当m=1时,n=0 其概率为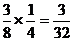
所以,甲获胜的概率为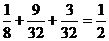
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com