
2.三角函数定义:角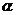 中边上任意一点
中边上任意一点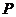 为
为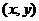 ,设
,设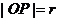 则:
则:
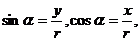
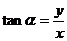
1.⑴角度制与弧度制的互化: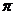 弧度
弧度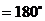 ,
,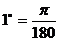 弧度,
弧度,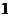 弧度
弧度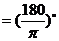
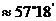
⑵弧长公式: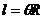 ;扇形面积公式:
;扇形面积公式: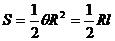 。
。
(二)导数
13.导数: ⑴导数定义:f(x)在点x0处的导数记作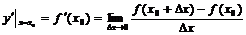 ;
;
⑵常见函数的导数公式: ①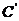
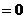 ;②
;②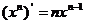 ;③
;③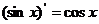 ;
;
④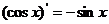 ;⑤
;⑤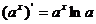 ;⑥
;⑥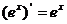 ;⑦
;⑦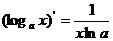 ;
;
⑧ 。
。
⑶导数的四则运算法则: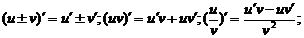
⑷(理科)复合函数的导数: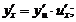
⑸导数的应用:
① 利用导数求切线:注意:ⅰ所给点是切点吗?ⅱ所求的是“在”还是“过”该点的切线?
②
利用导数判断函数单调性:ⅰ
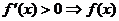 是增函数;
是增函数;
ⅱ 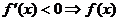 为减函数;ⅲ
为减函数;ⅲ 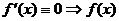 为常数;
为常数;
注:反之,成立吗?求单调区间,先求定义域。
③利用导数求极值:ⅰ求导数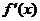 ;ⅱ求方程
;ⅱ求方程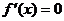 的根;ⅲ列表得极值。
的根;ⅲ列表得极值。
④利用导数最大值与最小值:ⅰ求的极值;ⅱ求区间端点值(如果有);ⅲ得最值。
⑤利用导数处理恒成立问题,证明不等式,解决实际应用问题
14.(理科)定积分
⑴定积分的定义: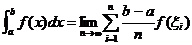
⑵定积分的性质:①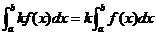 (
(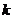 常数);
常数);
②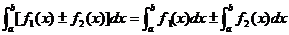 ;
;
③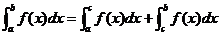 (其中
(其中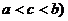 。
。
⑶微积分基本定理(牛顿-莱布尼兹公式):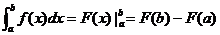
⑷定积分的应用:①求曲边梯形的面积: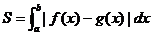 ;
;
①
求变速直线运动的路程: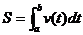 ;③求变力做功:
;③求变力做功: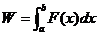 。
。
不等式
15.均值不等式: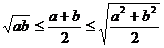
注意:①积定和最小,和定积最大,一正二定三相等;②变形,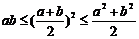 。
。
16.一元二次不等式
绝对值不等式: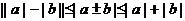
3.不等式的性质:
⑴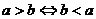 ;⑵
;⑵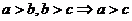 ;⑶
;⑶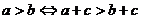 ;
;
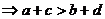 ;⑷
;⑷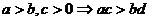 ;
;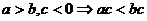 ;
;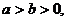
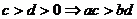 ;⑸
;⑸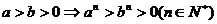 ;(6)
;(6)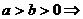
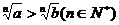 。
。
4.不等式等证明(主要)方法:⑴比较法:作差或作比;⑵综合法;⑶分析法。
(一)函数
1.映射:注意 ①第一个集合中的元素必须有象;②一对一,或多对一。
2.函数定义域的求法:函数解吸式有意义;符合实际意义;定义域优先原则
函数解析式的求法:代入法,凑配法,换元法,待定系数法,函数方程法
函数值域的求法:①分析法 ;②配方法 ;③判别式法 ;④利用函数单调性 ;
⑤换元法 ;⑥利用均值不等式 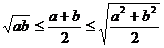 ; ⑦利用数形结合或几何意义(斜率、距离、绝对值的意义等);⑧利用函数有界性(
; ⑦利用数形结合或几何意义(斜率、距离、绝对值的意义等);⑧利用函数有界性(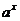 、
、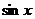 、
、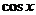 等);⑨导数法
等);⑨导数法
3.分段函数:值域(最值)、单调性、图象等问题,先分段解决,再下结论。
4.复合函数的有关问题(1)复合函数定义域求法:① 若f(x)的定义域为[a,b],则复合函数f[g(x)]的定义域由不等式a≤g(x)≤b解出② 若f[g(x)]的定义域为[a,b],求 f(x)的定义域,相当于x∈[a,b]时,求g(x)的值域。
(2)复合函数单调性的判定:①首先将原函数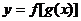 分解为基本函数:内函数
分解为基本函数:内函数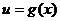 与外函数
与外函数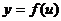 ;②分别研究内、外函数在各自定义域内的单调性;③根据“同性则增,异性则减”来判断原函数在其定义域内的单调性。
;②分别研究内、外函数在各自定义域内的单调性;③根据“同性则增,异性则减”来判断原函数在其定义域内的单调性。
注意:外函数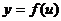 的定义域是内函数
的定义域是内函数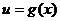 的值域。
的值域。
5.函数的奇偶性⑴函数的定义域关于原点对称是函数具有奇偶性的必要条件;
⑵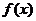 是奇函数
是奇函数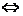
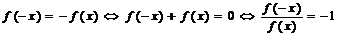 ;
;
⑶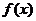 是偶函数
是偶函数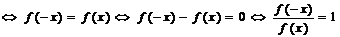 ;
;
⑷奇函数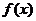 在原点有定义,则
在原点有定义,则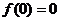 ;
;
⑸在关于原点对称的单调区间内:奇函数有相同的单调性,偶函数有相反的单调性;
(6)若所给函数的解析式较为复杂,应先化简,等价变形,再判断其奇偶性;
6.函数的单调性
⑴单调性的定义: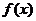 在区间
在区间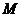 上是增(减)函数
上是增(减)函数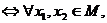 当
当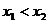 时
时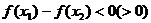
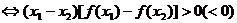
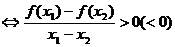 ;
;
⑵单调性的判定定义法:注意:一般要将式子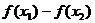 化为几个因式作积或作商的形式,以利于判断符号;②导数法(见导数部分);③复合函数法(见4(2)同增异减);④图像法。
化为几个因式作积或作商的形式,以利于判断符号;②导数法(见导数部分);③复合函数法(见4(2)同增异减);④图像法。
注:证明单调性要用定义法或导数法;求单调区间,先求定义域;多个单调区间之间不能用“并集”、“或”;单调区间不能用集合或不等式表示。
7.函数的周期性
(1)周期性的定义:对定义域内的任意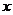 ,若有
,若有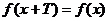 (其中
(其中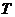 为非零常数),则称函数
为非零常数),则称函数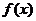 为周期函数,
为周期函数,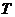 为它的一个周期。所有正周期中最小的称为函数的最小正周期。如没有特别说明,遇到的周期都指最小正周期。
为它的一个周期。所有正周期中最小的称为函数的最小正周期。如没有特别说明,遇到的周期都指最小正周期。
(2)三角函数的周期
①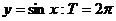 ;②
;②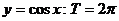 ;③
;③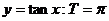 ;④
;④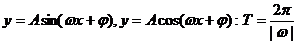 ;⑤
;⑤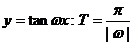 ;
;
⑶函数周期的判定:①定义法(试值) ②图像法 ③公式法(利用(2)中结论)
⑷与周期有关的结论:①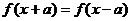 或
或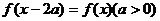
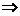
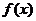 的周期为
的周期为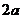 ;②
;②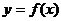 的图象关于点
的图象关于点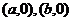 中心对称
中心对称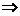
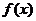 周期2
周期2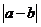 ;③
;③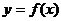 的图象关于直线
的图象关于直线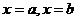 轴对称
轴对称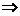
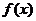 周期为2
周期为2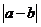 ;
;
④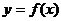 的图象关于点
的图象关于点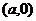 中心对称,直线
中心对称,直线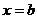 轴对称
轴对称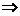
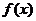 周期4
周期4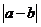 ;
;
8.幂、指、对的运算法则:
9.基本初等函数的图像与性质
⑴幂函数: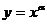 (
(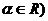 ;⑵指数函数:
;⑵指数函数: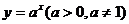 ;
;
⑶对数函数: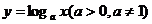 ;⑷正弦函数:
;⑷正弦函数: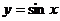 ;
;
⑸余弦函数: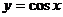 ;(6)正切函数:
;(6)正切函数: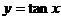 ;⑺一元二次函数:
;⑺一元二次函数: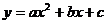 ;
;
⑻其它常用函数:①正比例函数: ;②反比例函数:
;②反比例函数: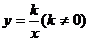 ;特别的
;特别的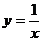 ,函数
,函数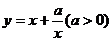 ;
;
10.二次函数:⑴解析式:①一般式: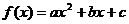 ;②顶点式:
;②顶点式: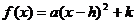 ,
,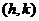 为顶点;③零点式:
为顶点;③零点式: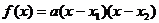 。
。
⑵二次函数问题解决需考虑的因素:①开口方向;②对称轴;③端点值;④与坐标轴交点;⑤判别式;⑥两根符号。⑶二次函数问题解决方法:①数形结合;②分类讨论。
11.函数图象
⑴图象作法 :①描点法(注意三角函数的五点作图)②图象变换法③导数法
⑵图象变换:
① 平移变换:ⅰ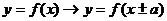 ,
,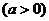 ---左“+”右“-”;
---左“+”右“-”;
ⅱ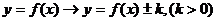 ---上“+”下“-”;
---上“+”下“-”;
② 伸缩变换:
ⅰ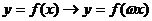 , (
, (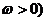 ---纵坐标不变,横坐标伸长为原来的
---纵坐标不变,横坐标伸长为原来的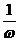 倍;
倍;
ⅱ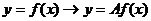 , (
, (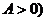 ---横坐标不变,纵坐标伸长为原来的
---横坐标不变,纵坐标伸长为原来的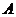 倍;
倍;
③ 对称变换:ⅰ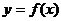
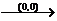
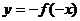 ;ⅱ
;ⅱ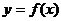
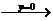
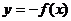 ;
;
ⅲ 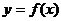
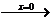
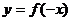 ; ⅳ
; ⅳ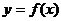
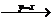
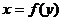 ;
;
④ 翻转变换:
ⅰ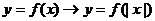 ---右不动,右向左翻(
---右不动,右向左翻(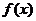 在
在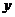 左侧图象去掉);
左侧图象去掉);
ⅱ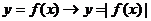 ---上不动,下向上翻(|
---上不动,下向上翻(|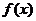 |在
|在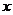 下面无图象);
下面无图象);
(3).函数图象(曲线)对称性的证明:
ⅰ证明函数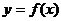 图像的对称性,即证明图像上任意点关于对称中心(对称轴)的对称点仍在图像上;
图像的对称性,即证明图像上任意点关于对称中心(对称轴)的对称点仍在图像上;
ⅱ证明函数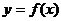 与
与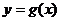 图象的对称性,即证明
图象的对称性,即证明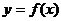 图象上任意点关于对称中心(对称轴)的对称点在
图象上任意点关于对称中心(对称轴)的对称点在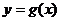 的图象上,反之亦然;
的图象上,反之亦然;
注:①曲线C1:f(x,y)=0关于点(a,b)的对称曲线C2方程为:f(2a-x,2b-y)=0;
②曲线C1:f(x,y)=0关于直线x=a的对称曲线C2方程为:f(2a-x, y)=0;
③曲线C1:f(x,y)=0,关于y=x+a(或y=-x+a)的对称曲线C2的方程为f(y-a,x+a)=0(或f(-y+a,-x+a)=0);④f(a+x)=f(b-x)
(x∈R) y=f(x)图像关于直线x=
y=f(x)图像关于直线x=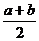 对称;
对称;
特别地:f(a+x)=f(a-x) (x∈R) y=f(x)图像关于直线x=a对称;
y=f(x)图像关于直线x=a对称;
⑤函数y=f(x-a)与y=f(b-x)的图像关于直线x=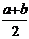 对称;
对称;
12.函数零点的求法:⑴直接法(求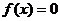 的根);⑵图象法;⑶二分法.
的根);⑵图象法;⑶二分法.
7. 全称量词与存在量词
全称量词与存在量词
⑴全称量词-------“所有的”、“任意一个”等,用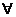 表示;
表示;
全称命题p: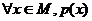 ; 全称命题p的否定
; 全称命题p的否定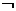 p:
p: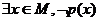 。
。
⑵存在量词--------“存在一个”、“至少有一个”等,用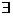 表示;
表示;
特称命题p: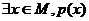 ; 特称命题p的否定
; 特称命题p的否定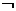 p:
p: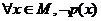 ;
;
6.逻辑连接词:






 ⑴且(and) :命题形式
p
⑴且(and) :命题形式
p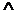 q; p q p
q; p q p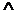 q p
q p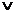 q
q 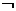 p
p
 ⑵或(or):命题形式 p
⑵或(or):命题形式 p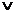 q; 真
真 真 真 假
q; 真
真 真 真 假
 ⑶非(not):命题形式
⑶非(not):命题形式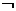 p .
真 假 假 真 假
p .
真 假 假 真 假
 假
真 假 真 真
假
真 假 真 真
 假 假 假 假 真
假 假 假 假 真
5.充要条件的判断:
(1)定义法----正、反方向推理;
(2)利用集合间的包含关系:例如:若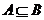 ,则A是B的充分条件或B是A的必要条件;若A=B,则A是B的充要条件;
,则A是B的充分条件或B是A的必要条件;若A=B,则A是B的充要条件;
4.四种命题:
⑴原命题:若p则q; ⑵逆命题:若q则p;
⑶否命题:若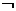 p则
p则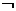 q;⑷逆否命题:若
q;⑷逆否命题:若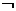 q则
q则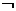 p
p
注:原命题与逆否命题等价;逆命题与否命题等价。判断命题真假时常常借助判断其逆否命题的真假
3.(1)含n个元素的集合的子集数为2n,真子集数为2n-1;非空真子集的数为2n-2;
(2)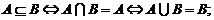 注意:讨论的时候不要遗忘了
注意:讨论的时候不要遗忘了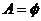 的情况;
的情况;
(3)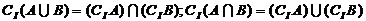 。
。
2.数形结合是解集合问题的常用方法:解题时要尽可能地借助数轴、直角坐标系或韦恩图等工具,将抽象的代数问题具体化、形象化、直观化,然后利用数形结合的思想方法解决,特别是在集合的交、并、补的运算之中。注意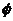 是任何集合的子集,是任何非空集合的真子集。注意补集思想的应用(反证法,对立事件,排除法等)。
是任何集合的子集,是任何非空集合的真子集。注意补集思想的应用(反证法,对立事件,排除法等)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com