
22.解:(1)设实数是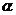 ,则
,则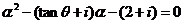 ,即
,即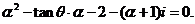
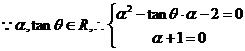 ,
,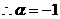 且
且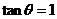 .
.
又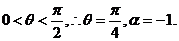
(2)证明:若方程有纯虚数根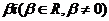 ,则
,则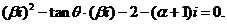
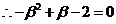 (1)且
(1)且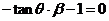 (2)
(2)
由(2)式得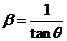 代入(1)式,得
代入(1)式,得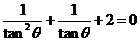 ,此方程
,此方程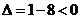 ,所以
,所以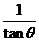 为虚数,与
为虚数,与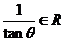 矛盾,故假设不成立。
矛盾,故假设不成立。
所以原方程对于任意的实数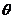 不可能有纯虚数根。
不可能有纯虚数根。
第四章 框图
第一讲 流程图
[知识梳理]
[知识盘点]
21.解: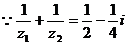 .
. 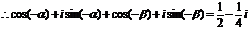

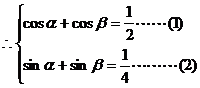
(1)2+(2)2得: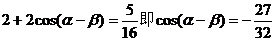
由(1)得: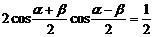 …………(3)
…………(3)
由(2)得: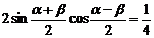 …………(4)
…………(4)
(4)÷(3)得: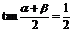
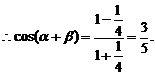
20.解:(1)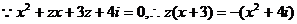
当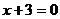 ,即
,即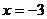 时,
时,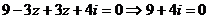 矛盾,所以
矛盾,所以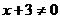 。
。
所以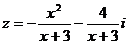 , 由题意
, 由题意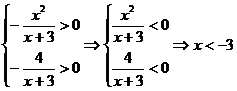
(2)假设存在这样的x,使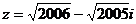 则
则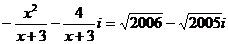 ,
,
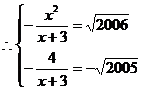 ,方程组无解,所以这样的x不存在。
,方程组无解,所以这样的x不存在。
19.解:因为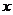 是实数,所以
是实数,所以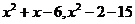 也是实数。从而
也是实数。从而
(1)当实数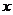 满足
满足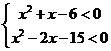 ,即
,即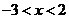 时,点Z在第三象限。
时,点Z在第三象限。
(2)当实数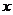 满足
满足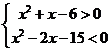 ,即
,即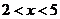 时,点Z在第四象限;
时,点Z在第四象限;
(3)当实数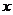 满足
满足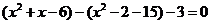 ,即
,即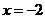 时,点Z在直线
时,点Z在直线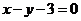 上。
上。
18.解:由题意得 z1=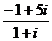 =2+3i,
=2+3i,
于是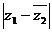 =
=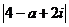 =
=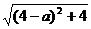 ,
,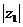 =
=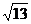 .
.
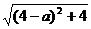 <
<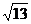 ,得a2-8a+7<0,1<a<7.
,得a2-8a+7<0,1<a<7.
17.解:由于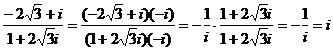 ;
;
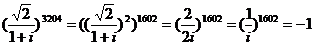 ;
;
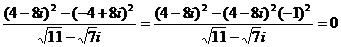 ;
;
从而 =0.
=0.
16.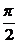
15.Z表示以点(1,0)为圆心,以2为半径的圆的内部或以(1,0)为圆心,8为半径的圆的外部
13.-1 14.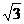 ,
, 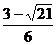
7.D 8.A 9.B 10.C 11.D 12.B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com